Animating Soil Models – Visualizations as open education tool for soil constitutive modeling
Contact: Gertraud Medicus – gertraud.medicus@uibk.ac.at
Acknowledgement: I thank the geotechnical engineers on Twitter, through whom I got the idea for this project. I am grateful for so much feedback and thank you all for your messages regarding the project. I further thank David Mašín for his support here on the platform SoilModels.com and Hans-Peter Schröcker (University of Innsbruck) for suggesting to use asymptote.sourceforge.io for the interactive graphics. I gratefully acknowledge financial support of the University of Innsbruck: ProLehre project, AURORA Challenge Domains. Project duration: 12/2020–11/2021, amount: € 13.808
The project was disseminated via soilmodels.com/soilanim, Twitter, LinkedIn, a newsletter and through publications and presentations.
english: ‘Animating Soil Models’: Animations as teaching and learning material for soil constitutive modeling. Webinar Series “Future of Geotechnical Education at the University Level, Ottawa, 2021-02-26.
english: Animating Soil Models – Visualizations as teaching and learning material for soil constitutive modeling. International Congress of Geotechnical Engineering GEOUPC / CIIGGUPC – 2022, Lima, 2022-10-13
english: The Use of Visualizations for Teaching Soil Constitutive Models. Sociedad Mexicana de Ingeniería Geotécnica AC /Sociedad Mexicana de Ingeniería Geotécnica, Mexiko-Stadt, 2021-08-16.
spanish: El uso de Visualizaciones para la enseñanza de Modelos Constitutivos del Suelo. Sociedad Mexicana de Ingeniería Geotécnica AC /Sociedad Mexicana de Ingeniería Geotécnica, Mexiko-Stadt, 2021-08-16.
Publications:
- Medicus, Gertraud; Ziotopoulou, Katerina; Huvey, Nejan (2023): Challenges and opportunities in teaching constitutive models in geotechnical courses. In: Zdravkovic, Lidija; Kontoe, Stavroula; Tsiampousi, Aikaterini; Taborda, David: Proceedings 10th NUMGE 2023. 10th European Conference on Numerical Methods in Geotechnical Engineering. 26 – 28 June 2023, London, UK. London: International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE)., No. 44. DOI: 10.53243/NUMGE2023-44
- Medicus, Gertraud (2022): Animating Soil Models: Visualisierungen von Stoffmodellen als offene Lehr- und Lernressource. In: Grabe, Jürgen: Workshop Numerische Methoden in der Geotechnik 2022, 12th & 13th of September 2022 Hamburg, Germany. Neumünster: Druckzentrum Neumünster GmbH (= Geotechnical Engineering and Construction Management, 53)., ISBN 978-3-936310-55-9, pp. 27 – 39. DOI: 10.15480/882.4607
- Medicus, Gertraud (2021): Teaching and Learning Critical State Constitutive Models with Animations. Canadian Geotechnique – The CGS Magazine, 2:3, Fall 2021
Presentations:
- Medicus, Gertraud; Ziotopoulou, Katerina; Huvey, Nejan: Challenges and opportunities in teaching constitutive models in geotechnical courses.
10th European Conference on Numerical Methods in Geotechnical Engineering (NUMGE 2023), London, UK, 2023-06-26. - Medicus, Gertraud: Visualizations as open education tool for soil constitutive modeling. University of North Carolina, North Carolina, 2023-02-24 (Online).
-
Medicus, Gertraud: Animating Soil Models – Visualizations as open education tool for soil constitutive modeling. University of Utah (UU), Salt Lake City, 2023-02-23 (Online).
- Medicus, Gertraud: Visualizations as teaching and learning material for soil constitutive modeling. Texas A&M Univerity, Texas, 2022-10-21 (Online).
- Medicus, Gertraud: Animating Soil Models – Visualizations as teaching and learning material for soil constitutive modeling. International Congress of Geotechnical Engineering GEOUPC / CIIGGUPC – 2022, Lima, 2022-10-13 (Online).
- Medicus, Gertraud: ‘Animating Soil Models’ – Visualizations as teaching and learning material for constitutive modelling. 32nd ALERT Workshop, Aussois, 2021-09-27. Posterpresentation
- Medicus, Gertraud: Animating Soil Models: Visualisierungen von Stoffmodellen als offene Lehr- und Lernressource. Numerische Methoden in der Geotechnik, Hamburg, 2022-09-12.
- Medicus, Gertraud: The Use of Visualizations for Teaching Soil Constitutive Models. Sociedad Mexicana de Ingeniería Geotécnica AC /Sociedad Mexicana de Ingeniería Geotécnica, Mexiko-Stadt, 2021-08-16 (Online).
- Medicus, Gertraud: Teaching and learning soil constitutive models with the help of visualisations. Univerzita Karlova v Praze / Charles University Prague / Karls-Universität Prag, Prag, 2021-04-26 (Online).
- Medicus, Gertraud: ‘Animating Soil Models’: Animations as teaching and learning material for soil constitutive modeling. Webinar Series “Future of Geotechnical Education at the University Level”, Ottawa, 2021-02-26 (Online).
… include the animations in LaTeX presentations:
Here you can download an example of how to include an animation in your beamer class presentation:
LaTeX_Beamer_Class
For every animation, you can download the related PDF file including all slides below each animation.
The PDF animations can be viewed with Acrobat Reader (except on mobile devices).
For Linux users:
Acroread 9 is availabe as Linux installation.
Okular 21.08.1 enables to watch the animations. However, the control buttons are not available using Okular.
Thanks to Wolfgang Fellin for trying out different PDF viewers for Linux.
The interactive graphic below has been created with GeoGebra
You can use the slider for parameter variation of M and choose to display Drucker-Prager. In addition, it is possible to move the principal stress state (red bullet) in the right figure and to rotate the 3D figure. The deviatoric plane corresponds to p = 100 kN/m².
click to enlarge
The interactive WebGL graphics below have been created using asymptote.sourceforge.io
click to enlarge
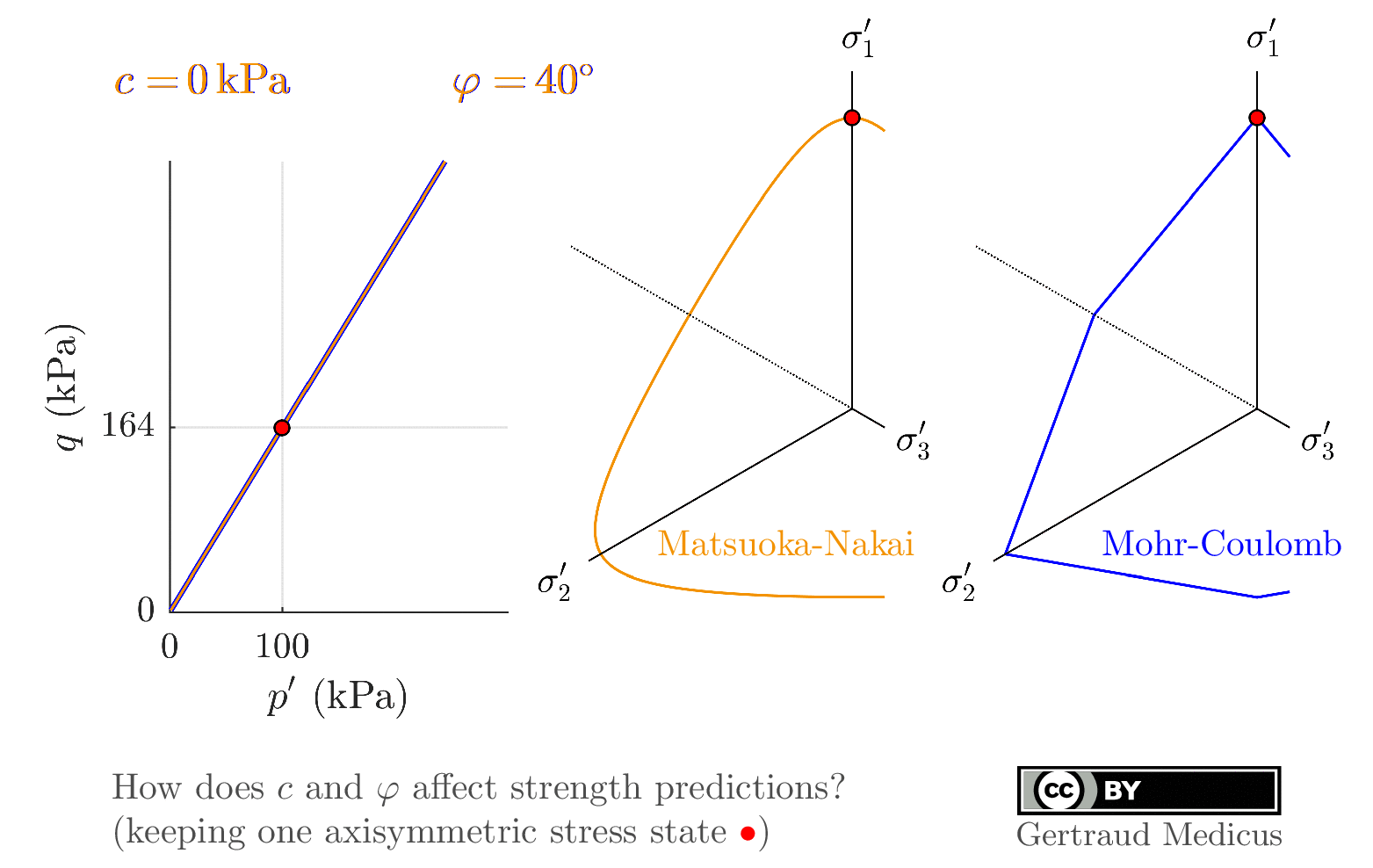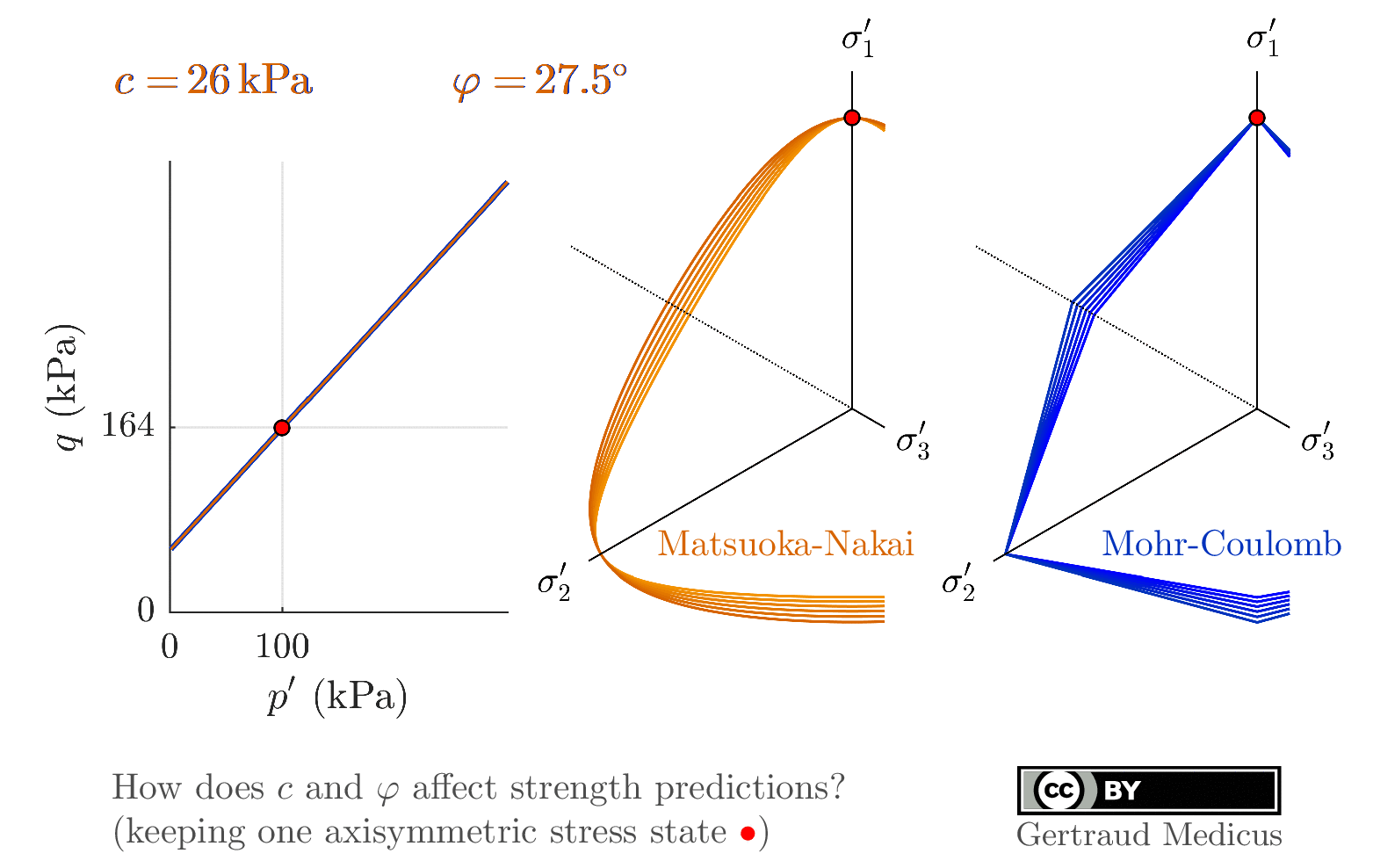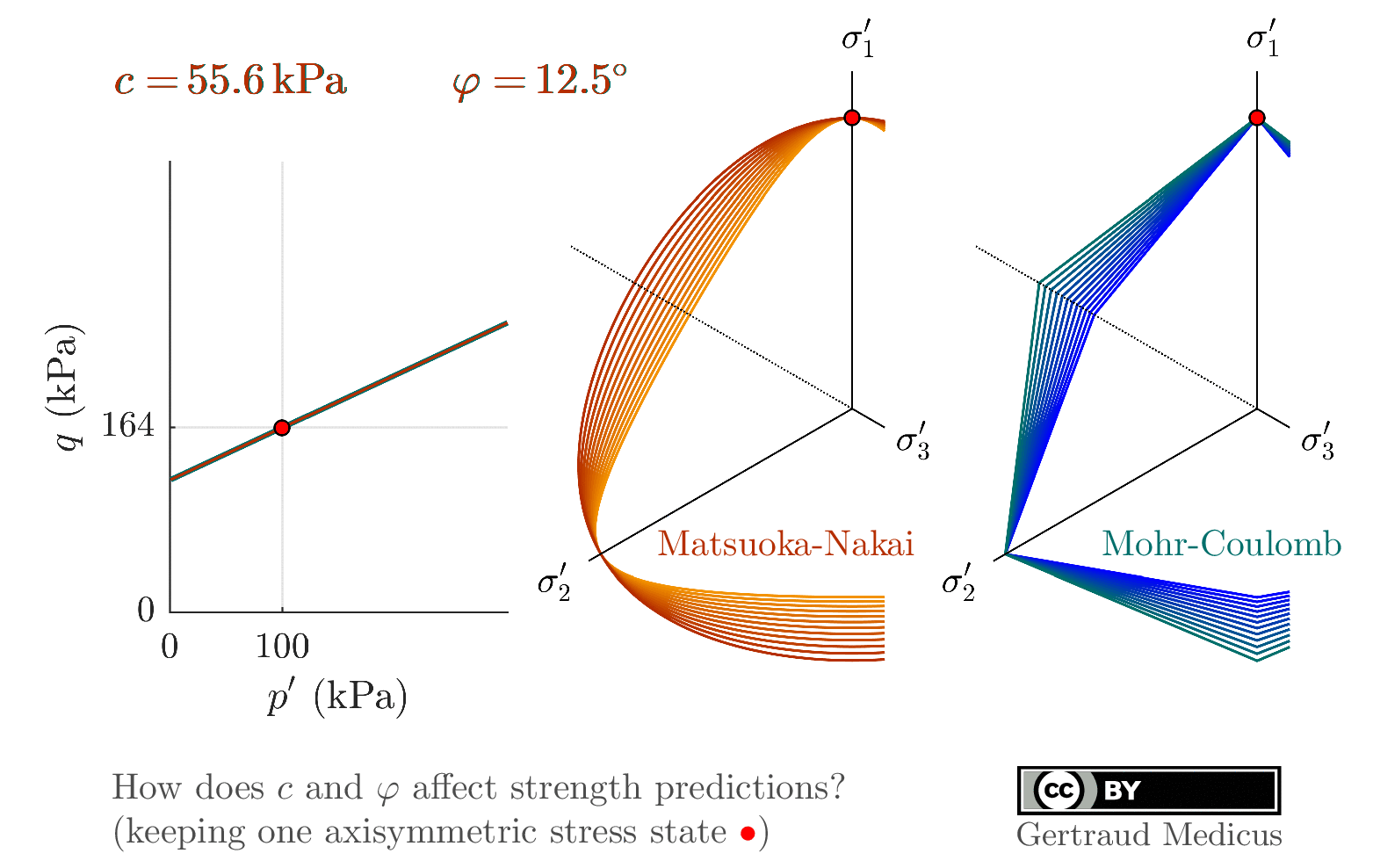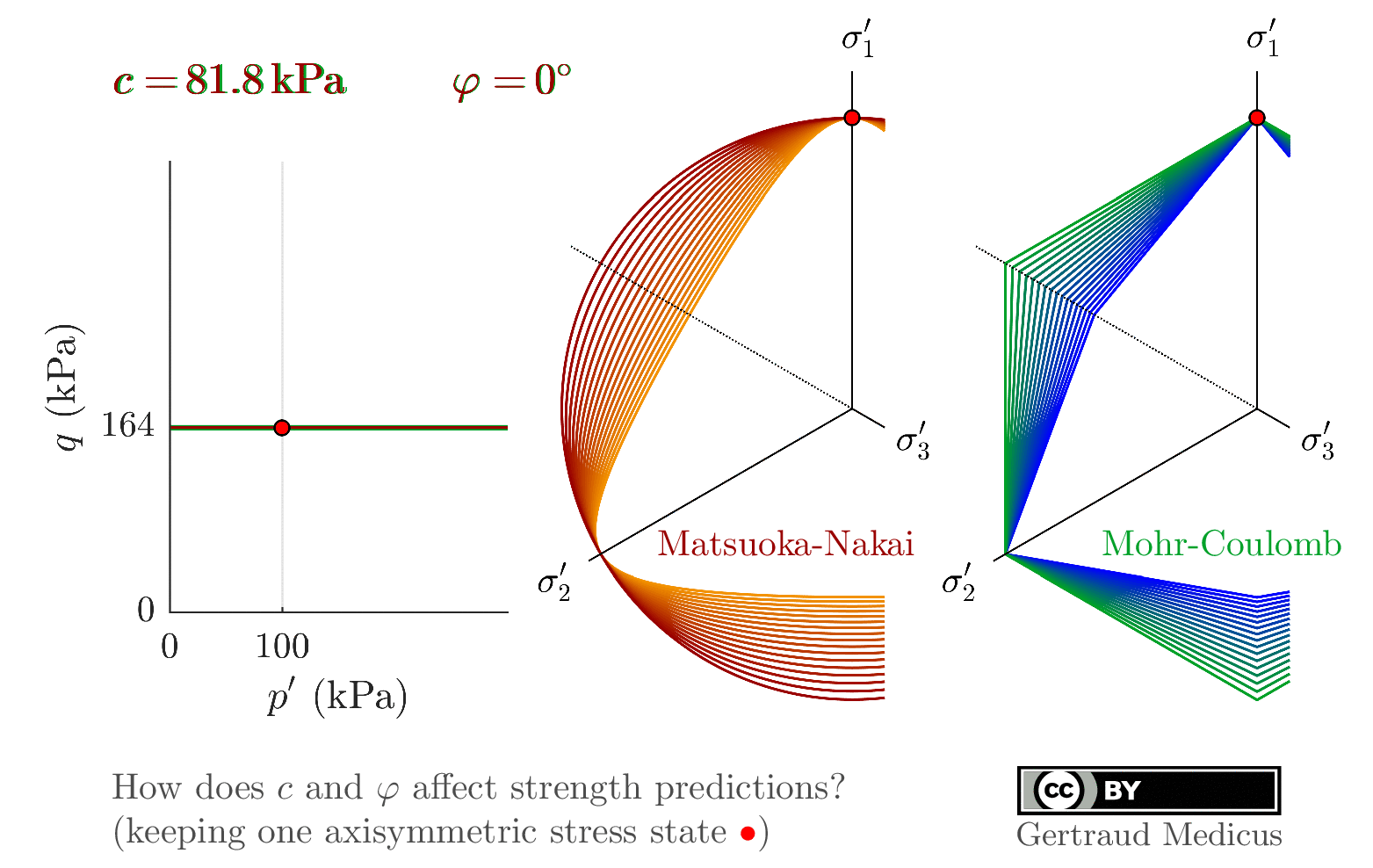
p-q plane (scaled) for axisymm. tr. comp. is added
click to enlarge
cohesion is added
click to enlarge
vizualise plane stress, σ₃=0
click to enlarge
Rendulic plane is added
click to enlarge
p-q plane (scaled) for axisymm. tr. comp. is added
click to enlarge
cohesion is added
click to enlarge
vizualise plane stress, σ₃=0
click to enlarge
Rendulic plane is added
click to enlarge
p-q plane (scaled) for axisymm. tr. comp. is added
click to enlarge
cohesion is added
click to enlarge
vizualise plane stress, σ₃=0
click to enlarge
Rendulic plane is added
click to enlarge
p-q plane (scaled) for axisymm. states is added
click to enlarge
vizualise plane stress, σ₃=0
click to enlarge
p-q plane (scaled) for axisymm. states is added
click to enlarge
vizualise plane stress, σ₃=0
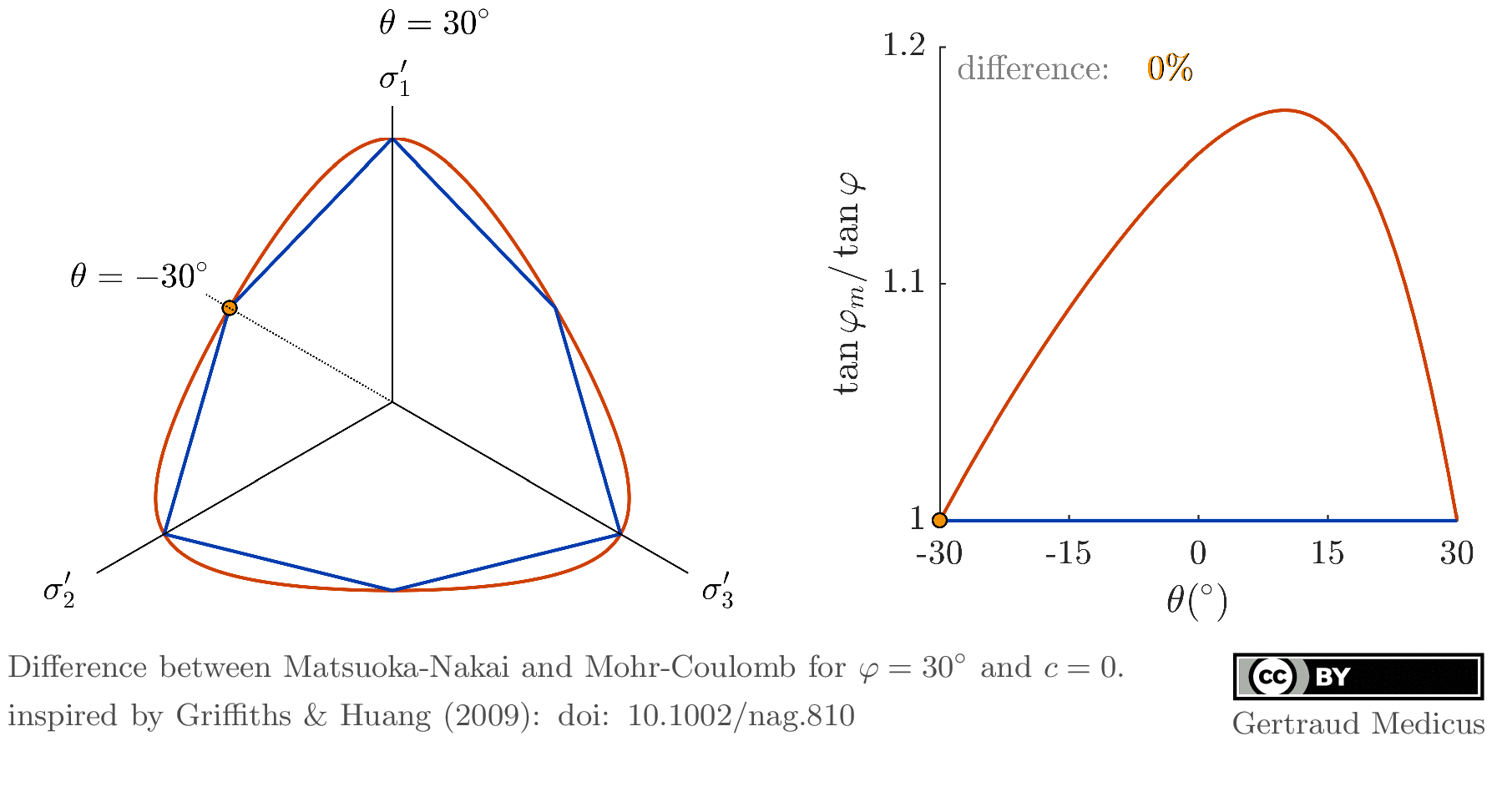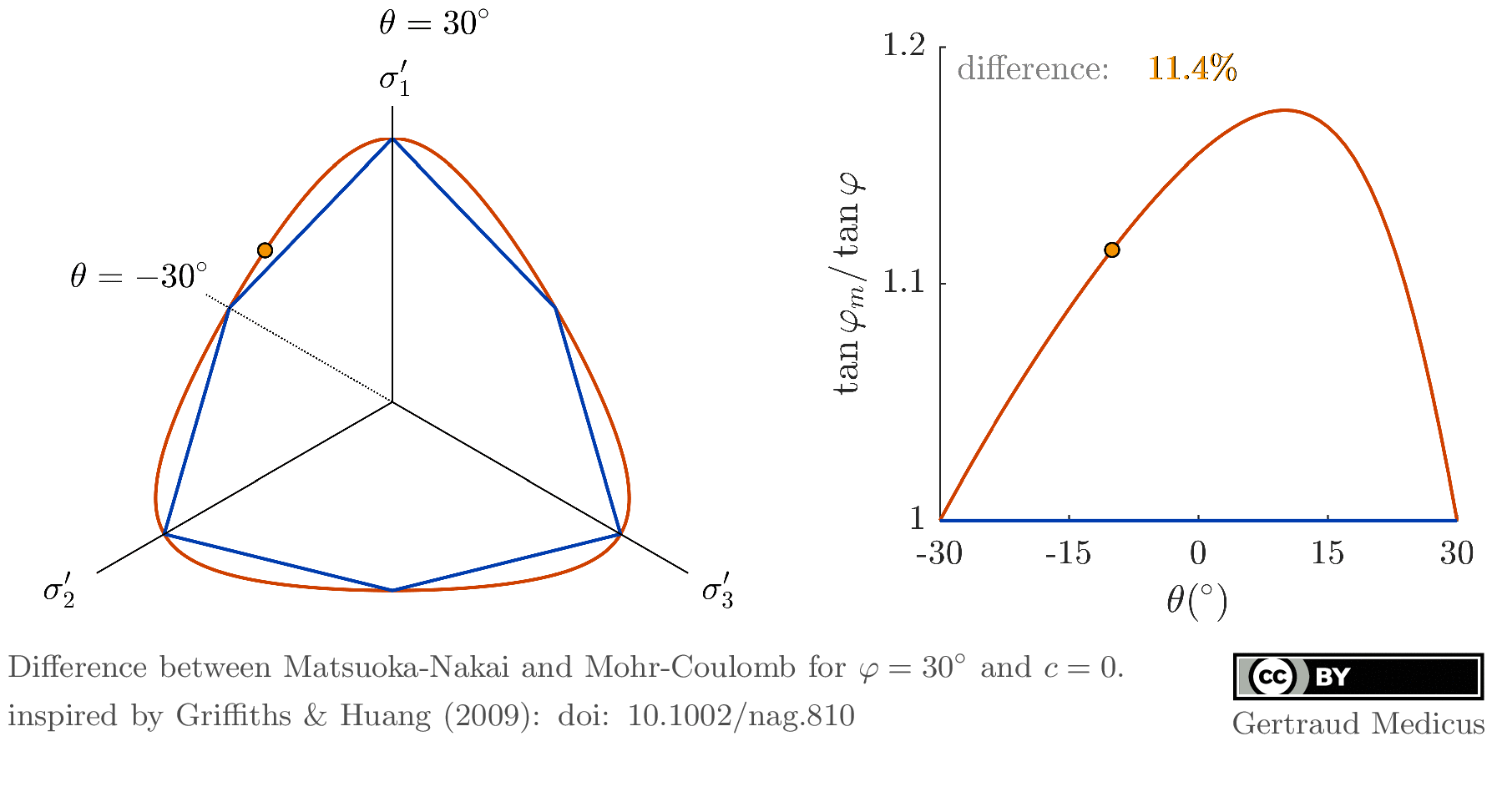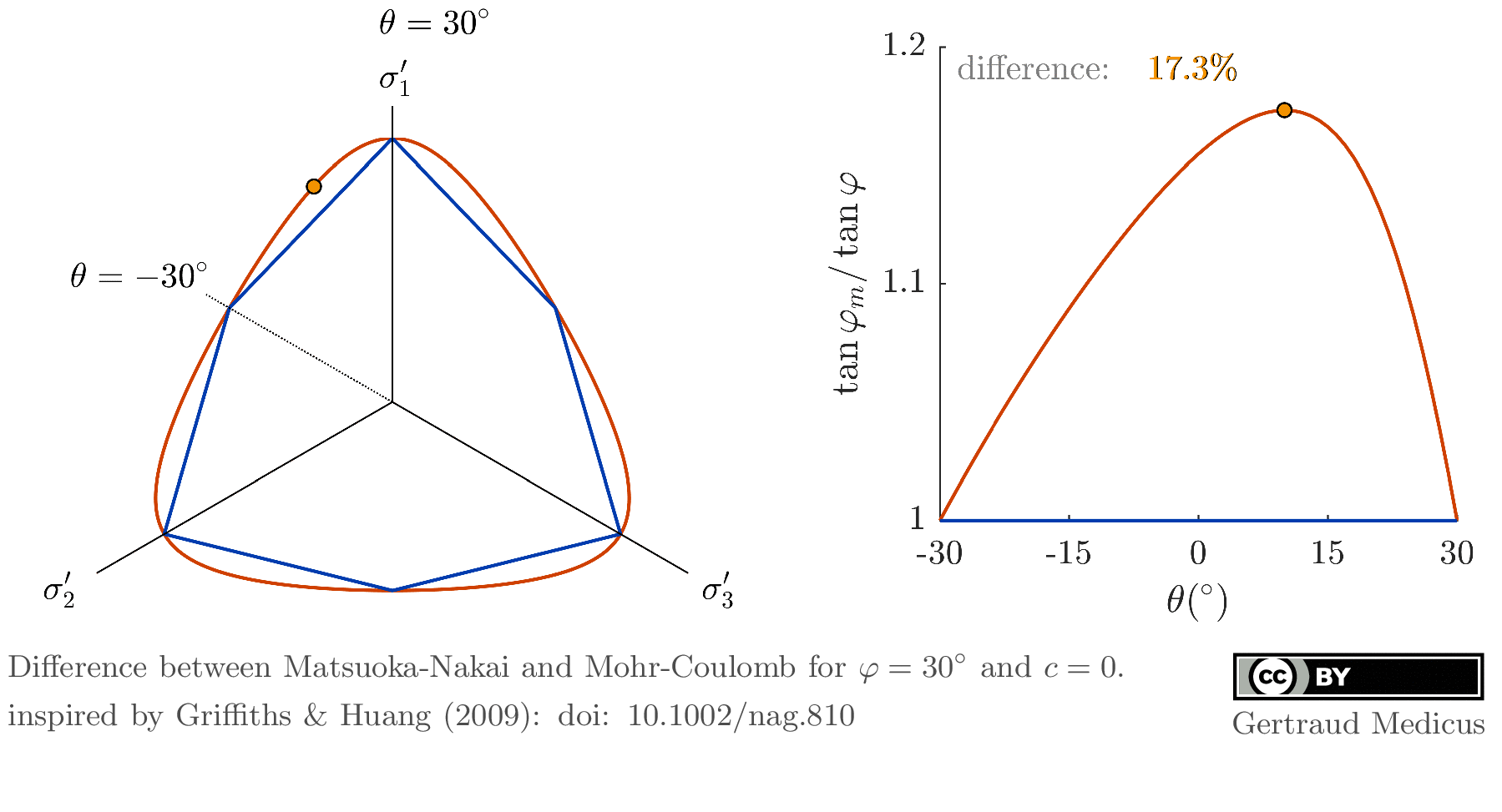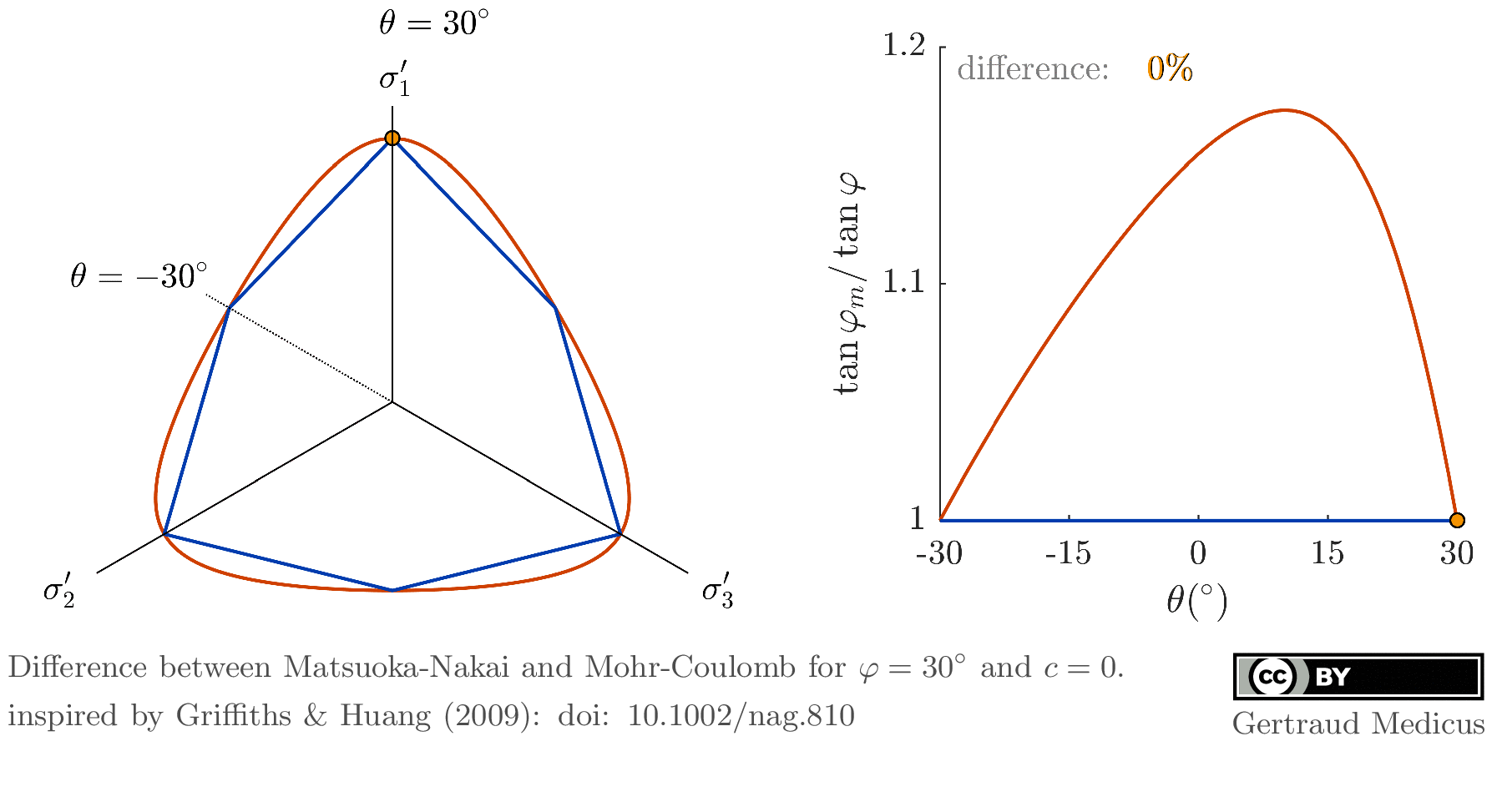
- Griffiths, D.V. (1990): Failure Criteria Interpretation Based on Mohr Coulomb Friction.
Journal of Geotechnical Engineering, Vol. 116, Issue 6.
doi: 10.1061/(ASCE)0733-9410(1990)116:6(986) - Griffiths, D.V. and Huang, J. (2009): Observations on the extended Matsuoka–Nakai failure criterion.
Int. J. Numer. Anal. Meth. Geomech., 33: 1889-1905.
doi: 10.1002/nag.810
The interactive graphics below have been created with GeoGebra
You can use the slider for variation of the radius. In addition, it is possible to move the point A (blue bullet) and the center C (black bullet). Sign convention: Tensile stresses (+), compressive stresses (-), for more details on sign convention, see for example Mang & Hofstetter (2013).
click to enlarge, the Figure is based on Mang & Hofstetter (2013)
This figure might help to illustrate the link between Mohr’s circles and stress paths, using a conventional drained triaxial compression test. The Mohr-Coulomb failure line for c=0 is shown and the stress state can be adjusted using the slider.
for mechanical sign convention, tensile stresses (+), compressive stresses (-): click to enlarge
for geotechnical sign convention, tensile stresses (-), compressive stresses (+): click to enlarge
Use the sliders to vary the parameters c and φ. You can also adjust the minor principal stress σ₃ for a given σ₁=-100 kPa until the Mohr-Coulomb failure criterion is reached.
for mechanical sign convention, tensile stresses (+), compressive stresses (-): click to enlarge
for geotechnical sign convention, tensile stresses (-), compressive stresses (+): click to enlarge
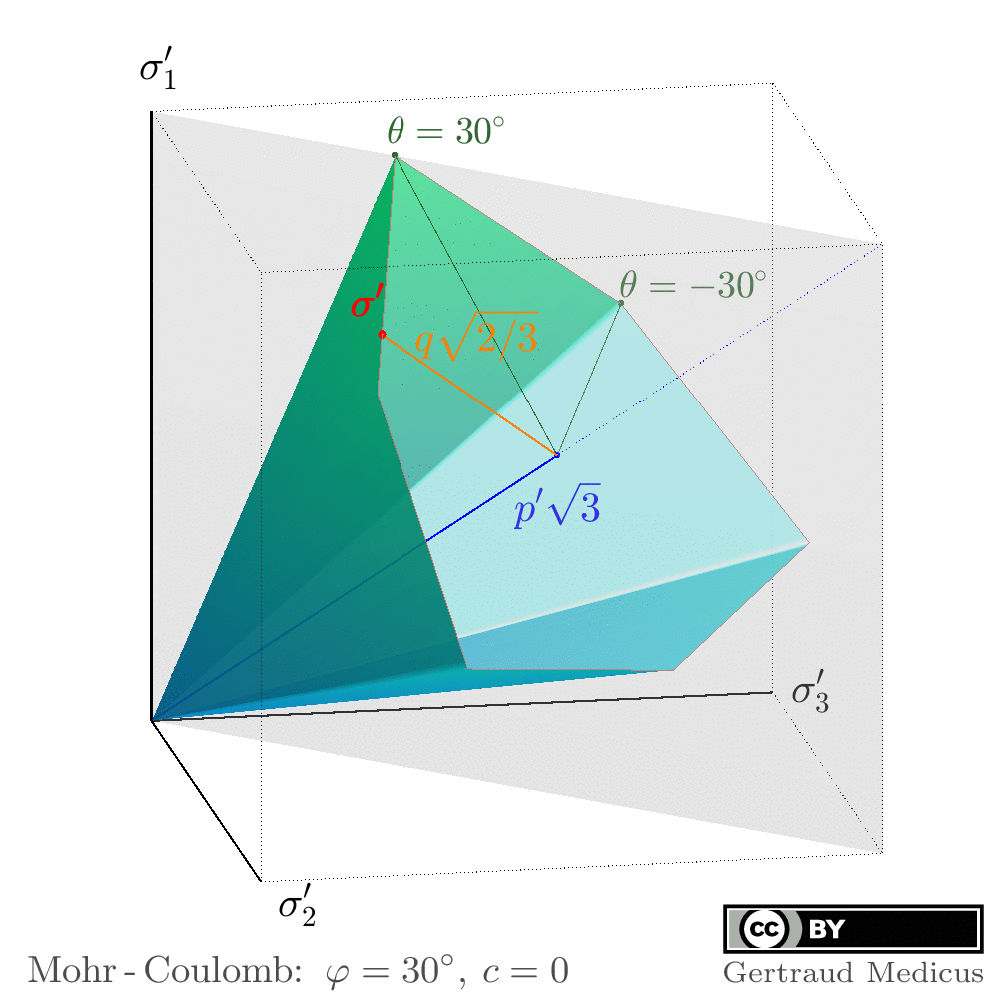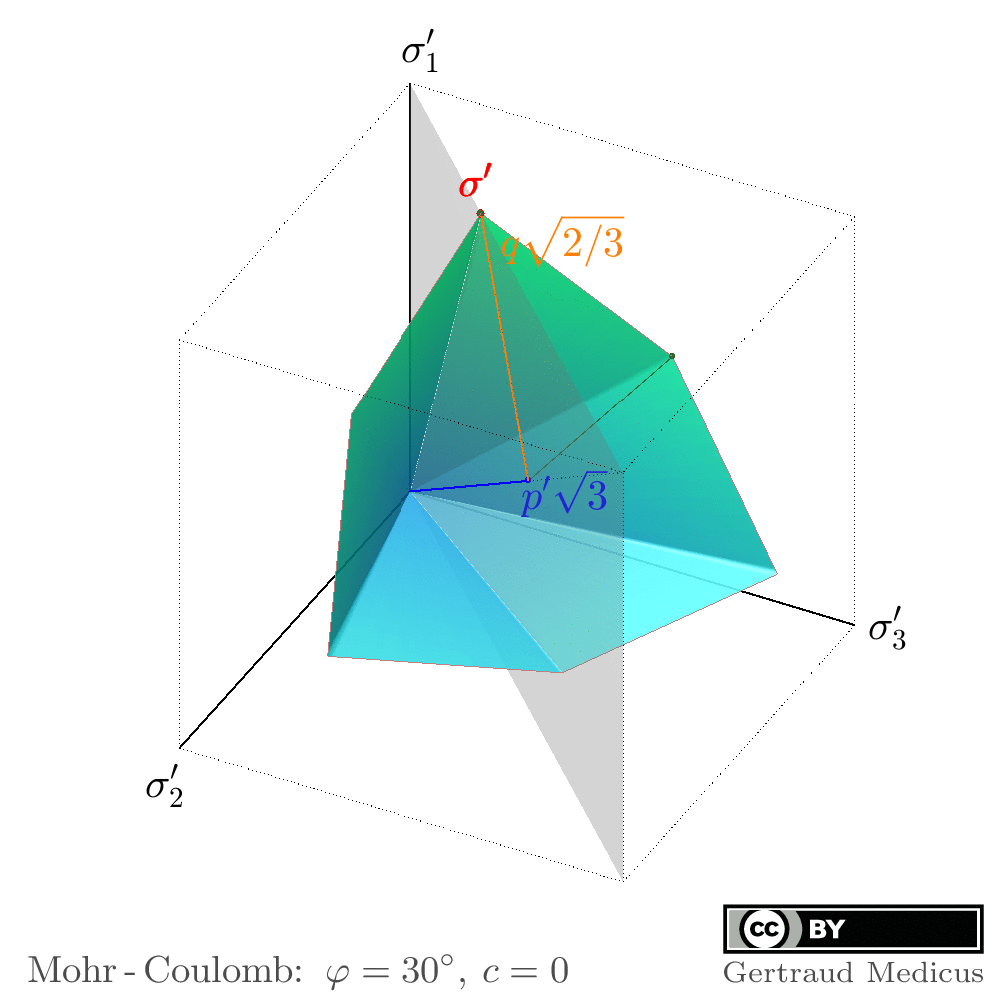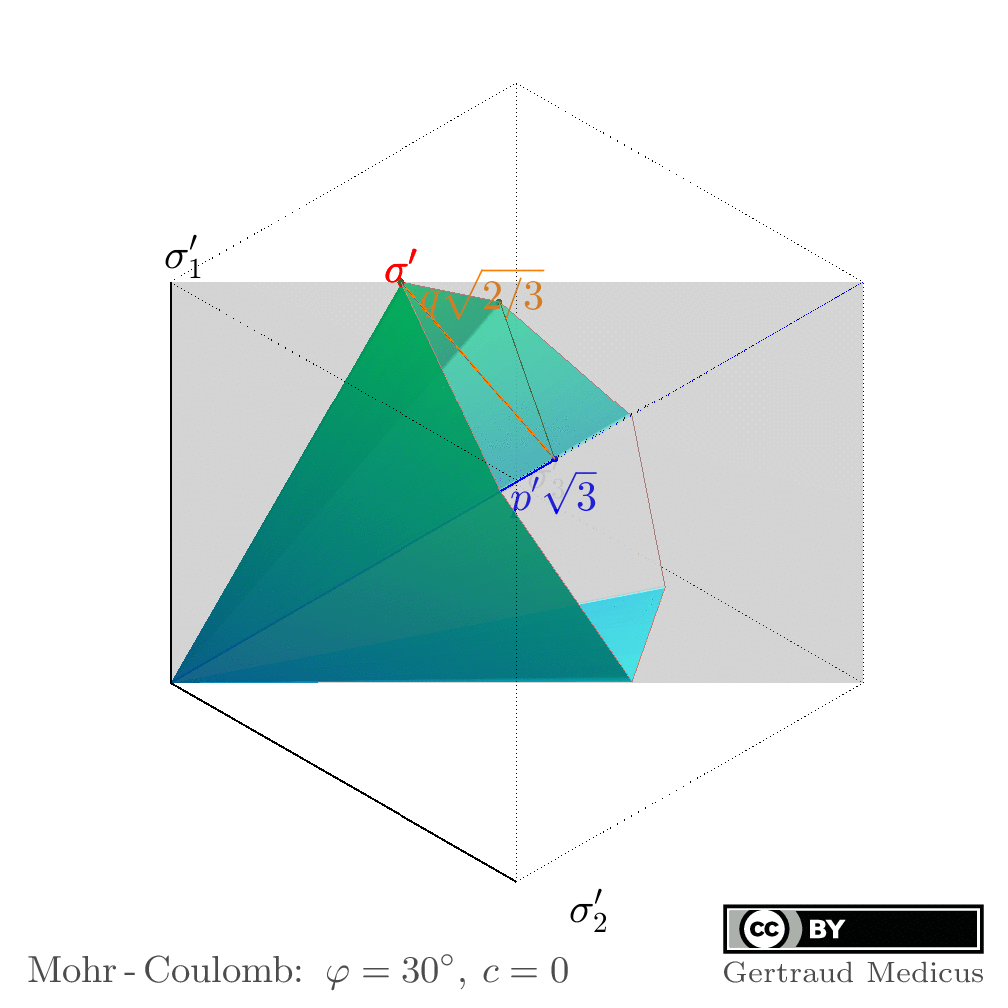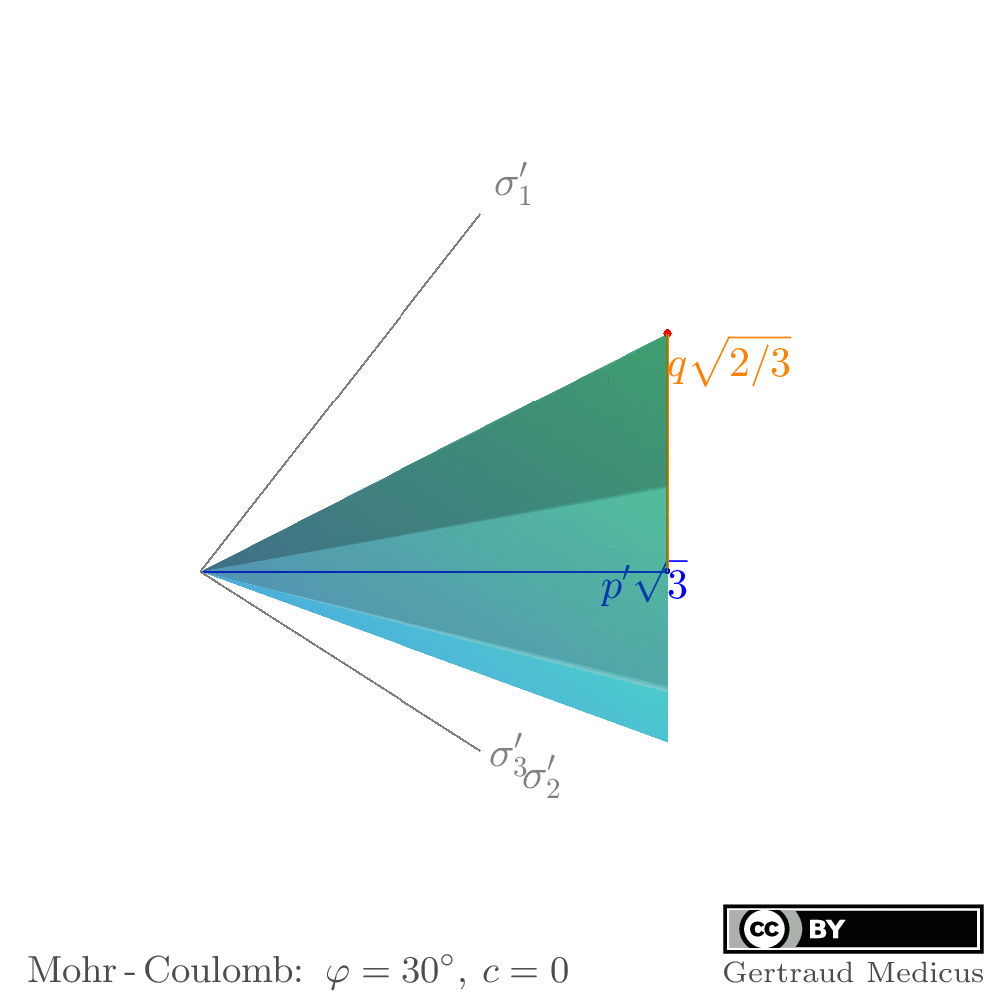
Animations to visualize the stress invariants in principal stress space:
p’: mean effective stress
q: deviatoric stress
θ: the Lode angle to define the deviatoric direction of a stress state
- PDF animation
- PDF file which includes all slides
- MATLAB scripts for 3D plots of Matsuoka-Nakai, Mohr-Coulomb and Drucker-Prager: MN_MC_DP.zip
Interactive WebGL graphics, created with asymptote.sourceforge.io
The interactive graphic below has been created with GeoGebra
You can use the yellow sliders for parameter variation. You can also vary the values for the mobilized friction angle φₘ (green) and Hvorslev’s equivalent pressure p’ₑ (black) and display the corresponding asymptotic states. In addition, it is possible to rotate the 3D figure. The ASBS is displayed for 1 < p’ₑ < 100 kN/m².
click to enlarge
The interactive graphic below has been created with GeoGebra
You can use the green sliders for parameter variation. You can also vary the value for the preconsolidation pressure p’₀ (black) and display the corresponding yield surface. In addition, it is possible to rotate the 3D figure. The SBS is displayed for 1 < p’₀ < 100 kN/m².
click to enlarge
This page related to SANISAND has been created in cooperation between Gertraud Medicus (University of Innsbruck, Austria) and Mahdi Taiebat (University of British Columbia, Canada).
The interactive graphics below have been created with GeoGebra
Yield surface: the model uses a Drucker-Prager yield surface with anisotropy. The isotropic size is controlled by model constant m and the anisotropy is controlled by internal variable α. You can adjust the related parameters and visualize the yield surface in the 3D stress Principal Axes space and in the π-plane for the stress-ratio, where co-axiality (i.e., same Principal Axes) of stress and back-stress tensors are implied.
Critical, dilatancy, and bounding surfaces: The model uses a fixed Lode angle dependent critical state surface, and state parameter dependent dilatancy and bounding surfaces. All three surfaces are isotropic. The size of the critical state surface is controlled by model constants M and c, the state parameter ψ adjusts the sizes of the dilatancy and bounding surfaces through model parameters nd and nb, respectively. You can adjust the related parameters and visualize the model surfaces in the 3D principal stress space.
click to enlarge
MATLAB scripts for Drucker-Prager yield surface with anisotropy and all SANISAND surfaces: sanisand.zip
The SANISAND-MSf (Yang, Taiebat & Dafalias, 2022) model includes two novel constitutive ingredients to address primarily the undrained cyclic response:
- A memory surface (M), resulting in an evolving distance quantity bM, for more precisely controlling stiffness affecting the plastic deviatoric and volumetric strains and ensuing excess pore pressure development in the pre-liquefaction stage.
- The concept of a semifluidised state (Sf) and the related formulation of an internal degradation variable for plastic modulus and dilatancy, named the ‘strain liquefaction factor’ and symbolled as l, aiming at modelling large shear strain development in the post-liquefaction stage.
The animation of the model simulation for Fig. 13 of the reference paper are illustrated below.
The interactive graphic below has been created with asymptote.sourceforge.io
The yield, dilatancy, critical state, bounding and memory surfaces according to SANISAND-MSf model are visualized in the 3D stress space below.
click to enlarge
Key reference:
- Yang, M., Taiebat, M. & Dafalias Y. F., SANISAND-MSf: a sand plasticity model with memory surface and semifluidised state, Géotechnique, 2022, 72:3, 227-24, doi: 10.1680/jgeot.19.P.363
Other references:
- Manzari, M. T. & Dafalias, Y. F. (1997). A critical state two-surface plasticity model for sands. Géotechnique 47, No. 2, 255–272.
- Dafalias, Y. F. & Manzari, M. T. (2004). Simple plasticity sand model accounting for fabric change effects. J. Engng Mech. 130, No. 6, 622–634.
- Taiebat, M. & Dafalias, Y. F. (2008). SANISAND: simple anisotropic sand plasticity model. Int. J. Numer. Analyt. Methods Geomech. 32, No. 8, 915–948.
- Dafalias, Y. F. & Taiebat, M. (2016). SANISAND-Z: zero elastic range sand plasticity model. Géotechnique 66, No. 12, 999–1013
- Barrero, A. R., Taiebat, M. & Dafalias, Y. F. (2020). Modeling cyclic shearing of sands in semifluidized regime. Int. J. Numer. Analyt. Methods Geomech. 44, No. 3, 371–388.
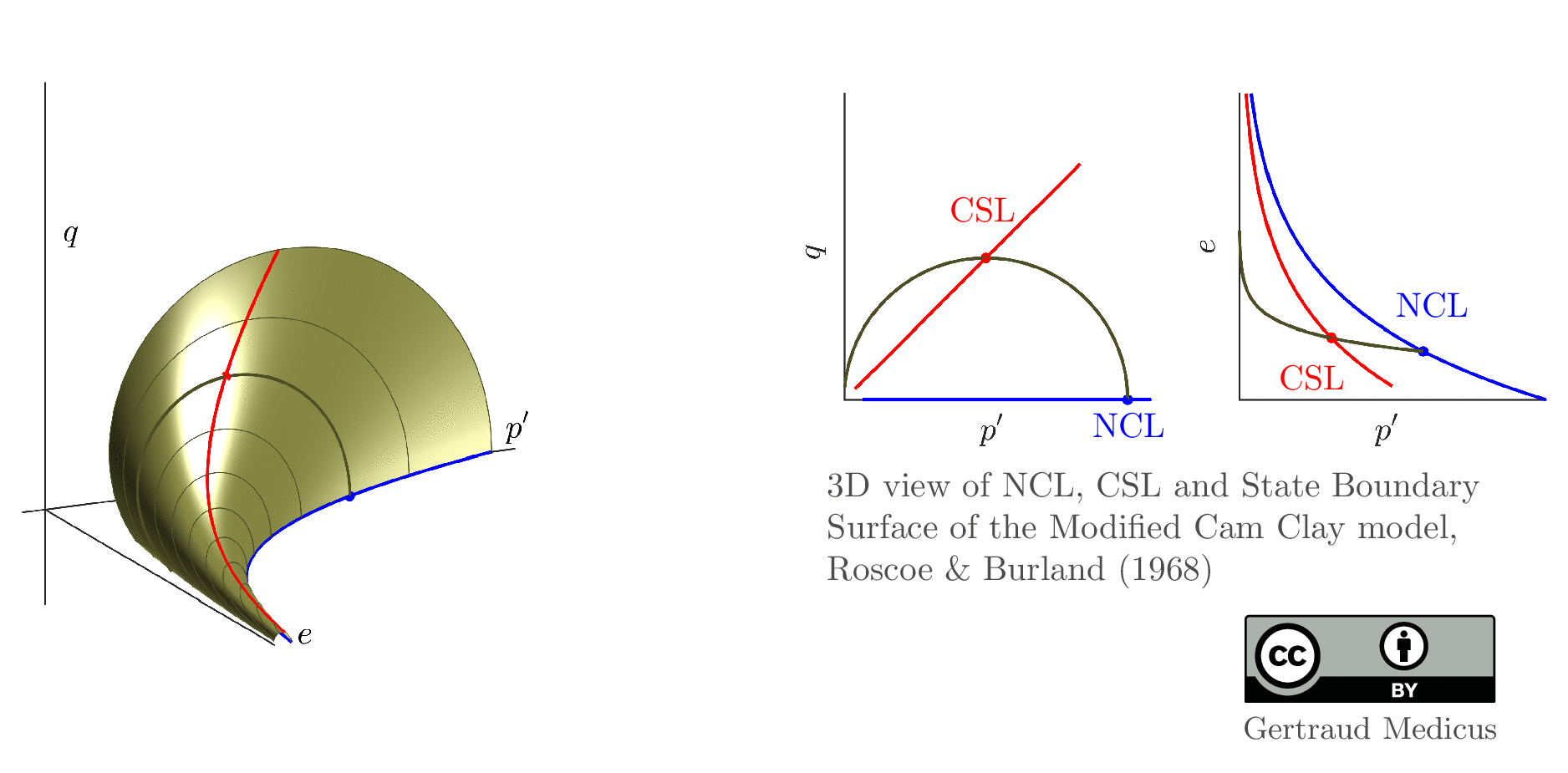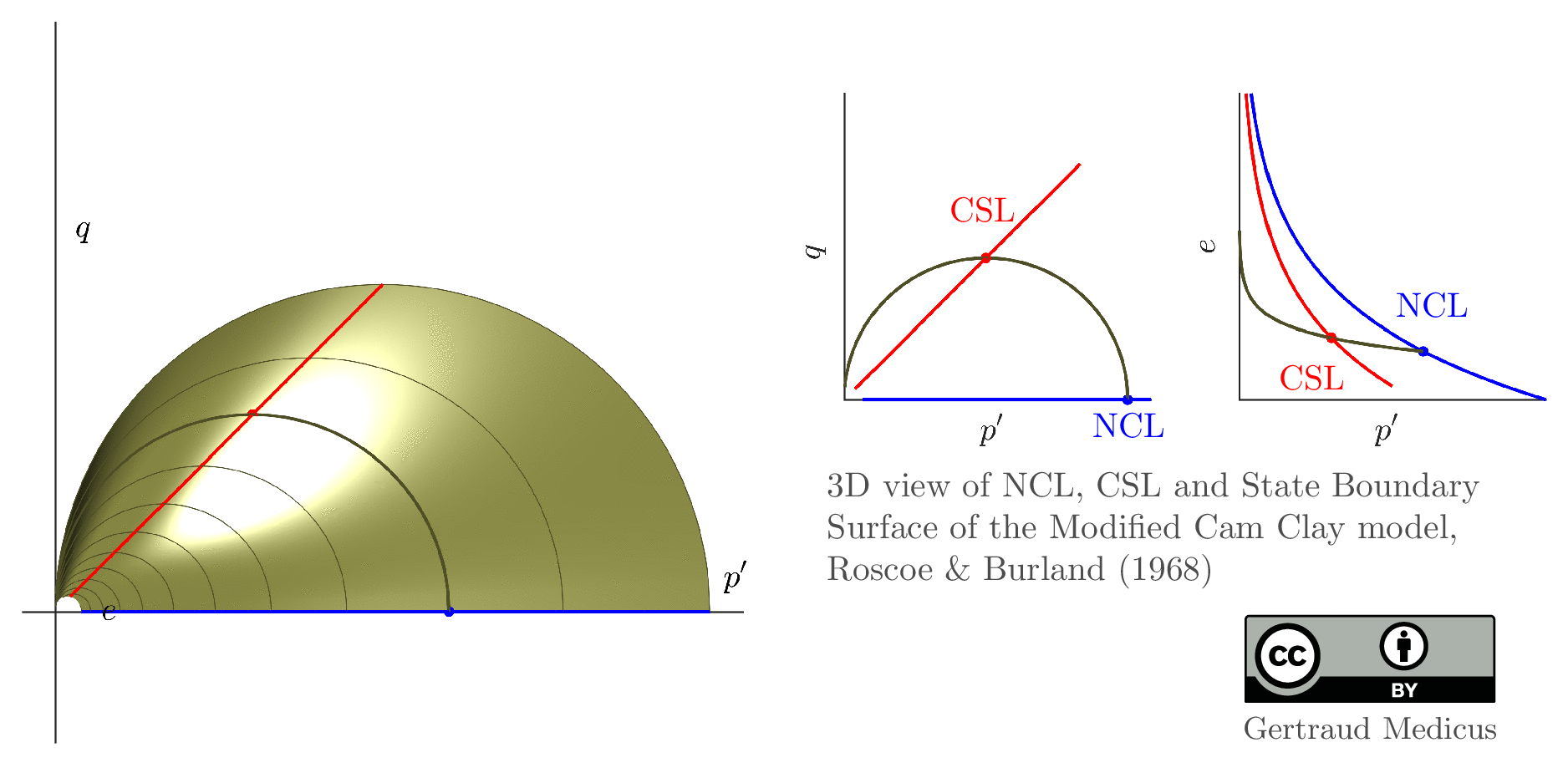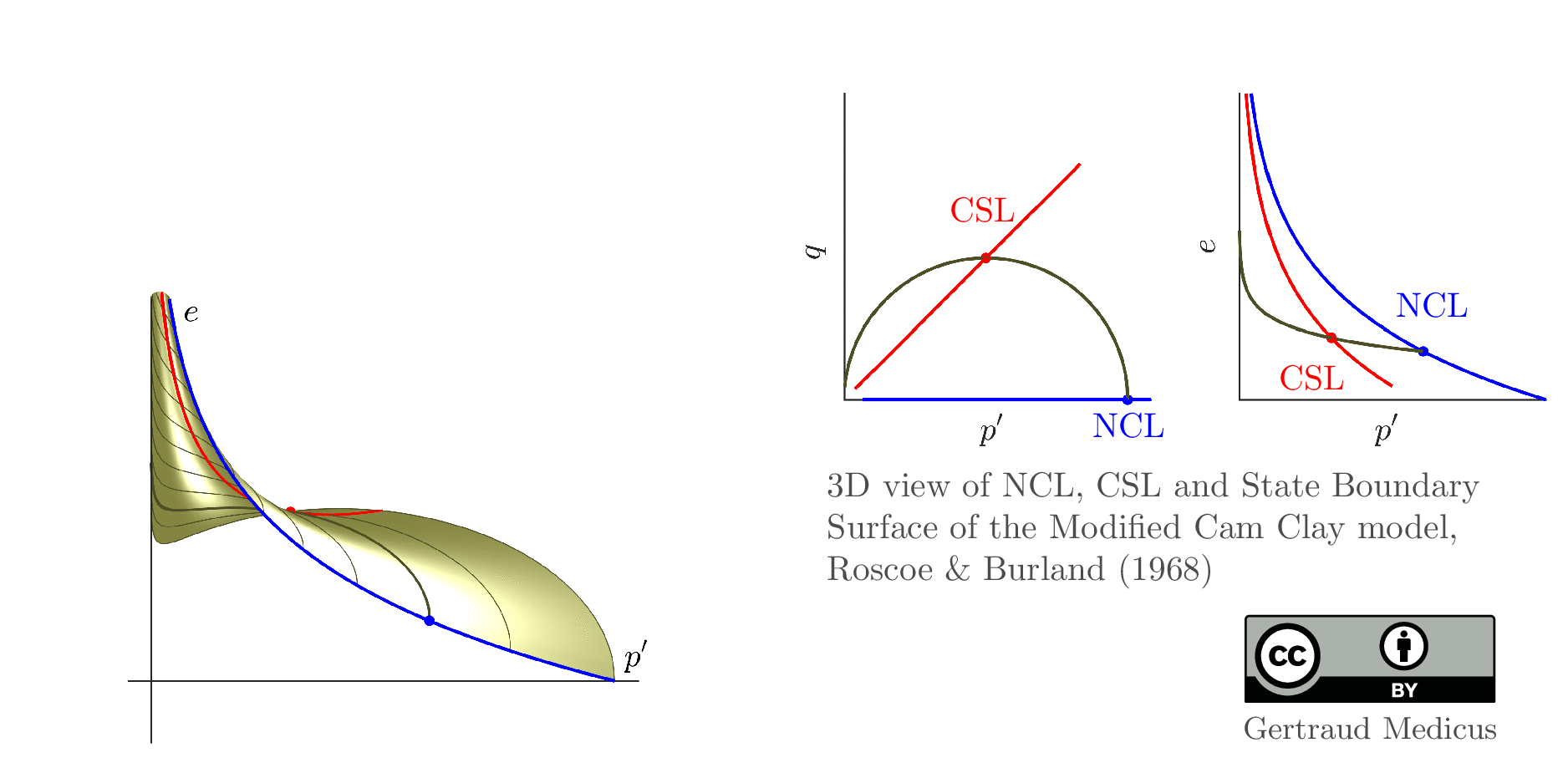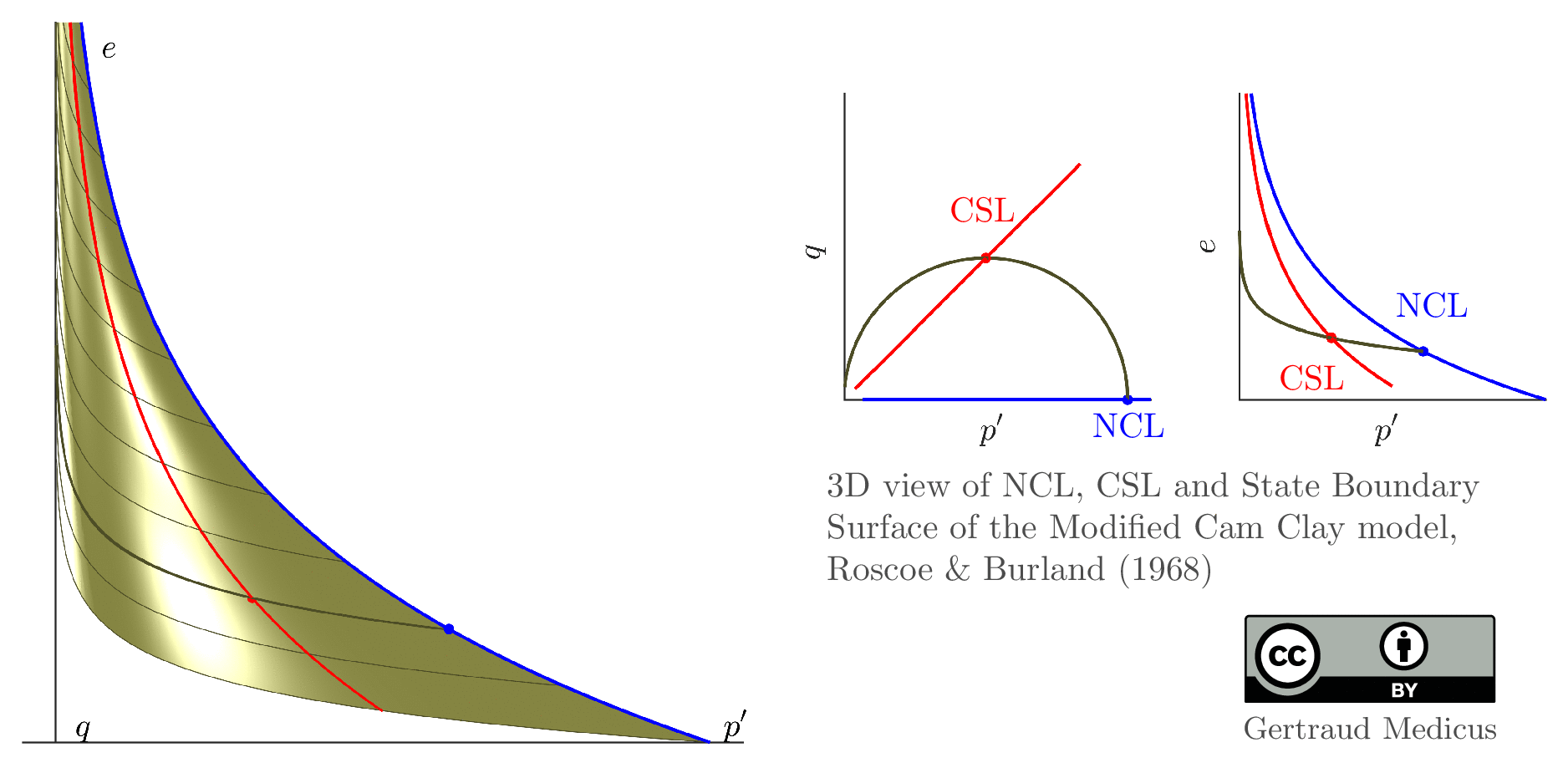
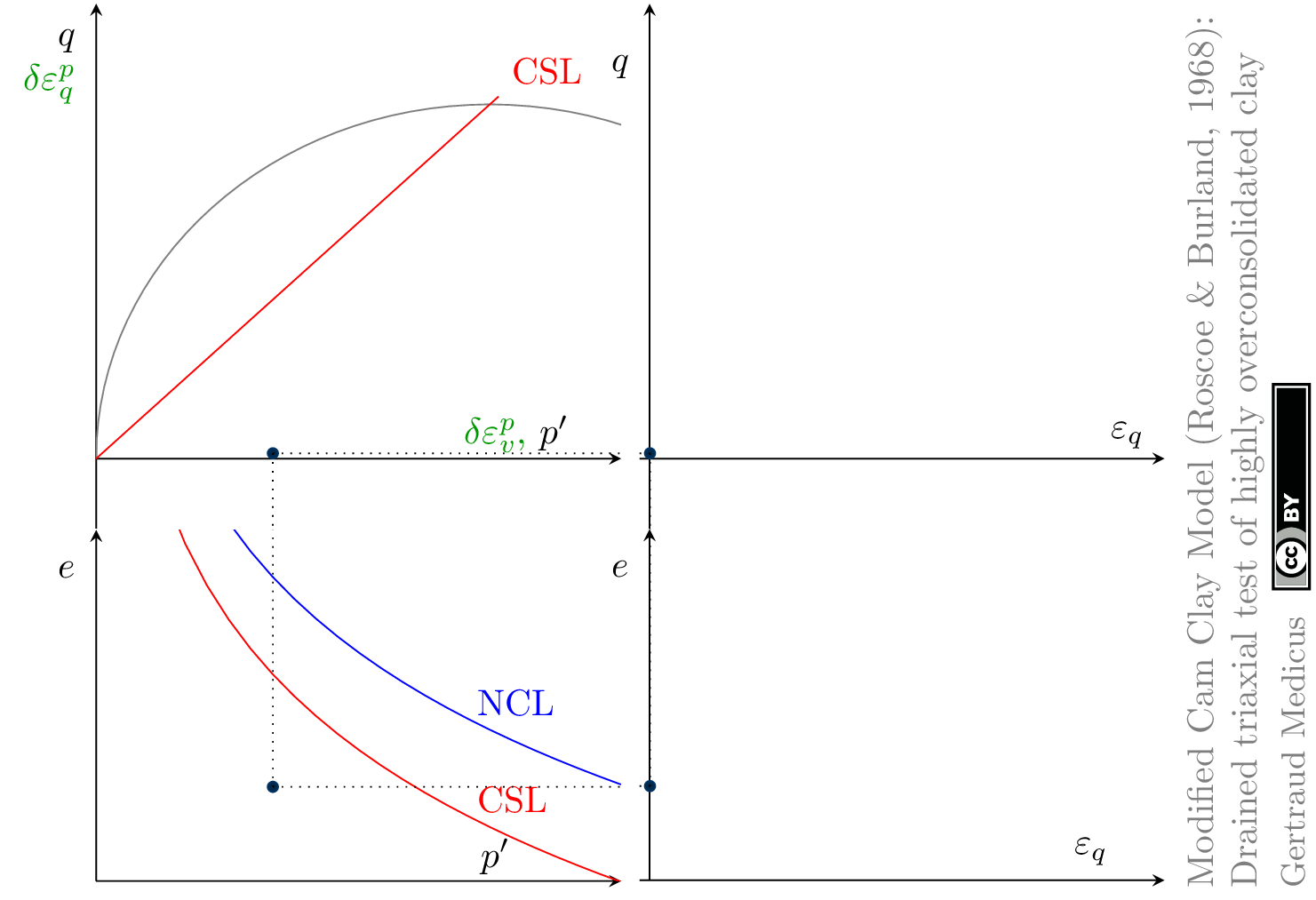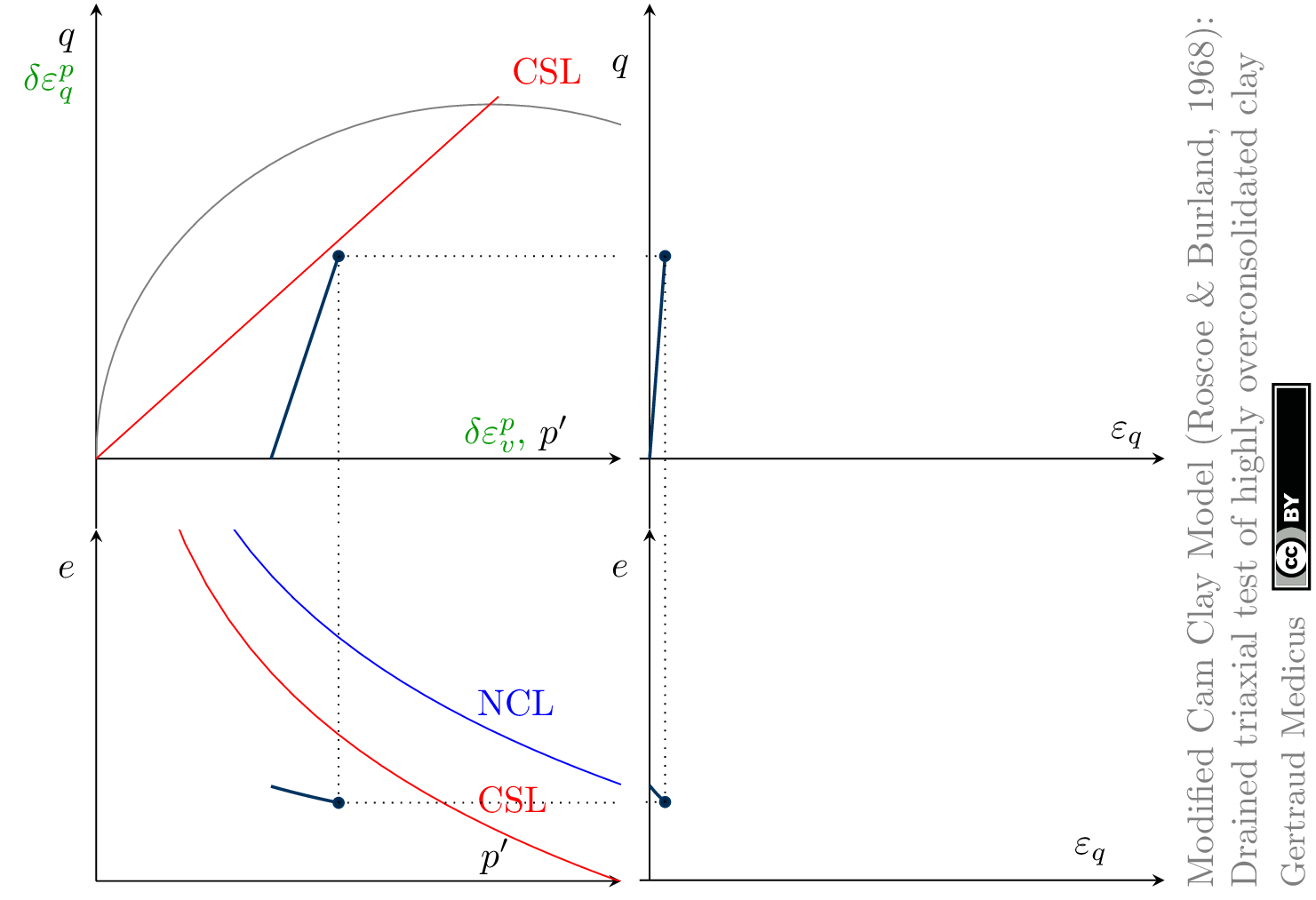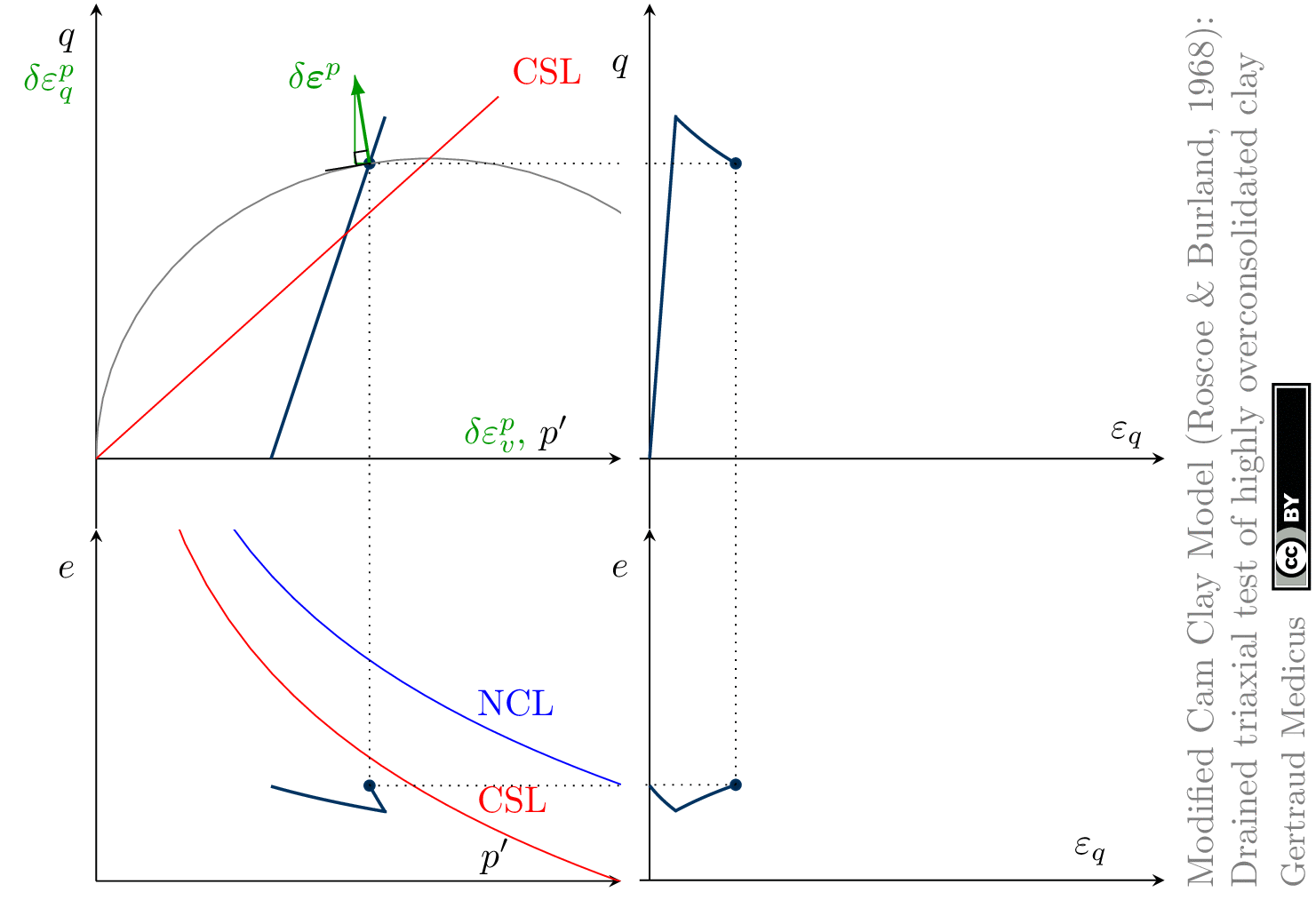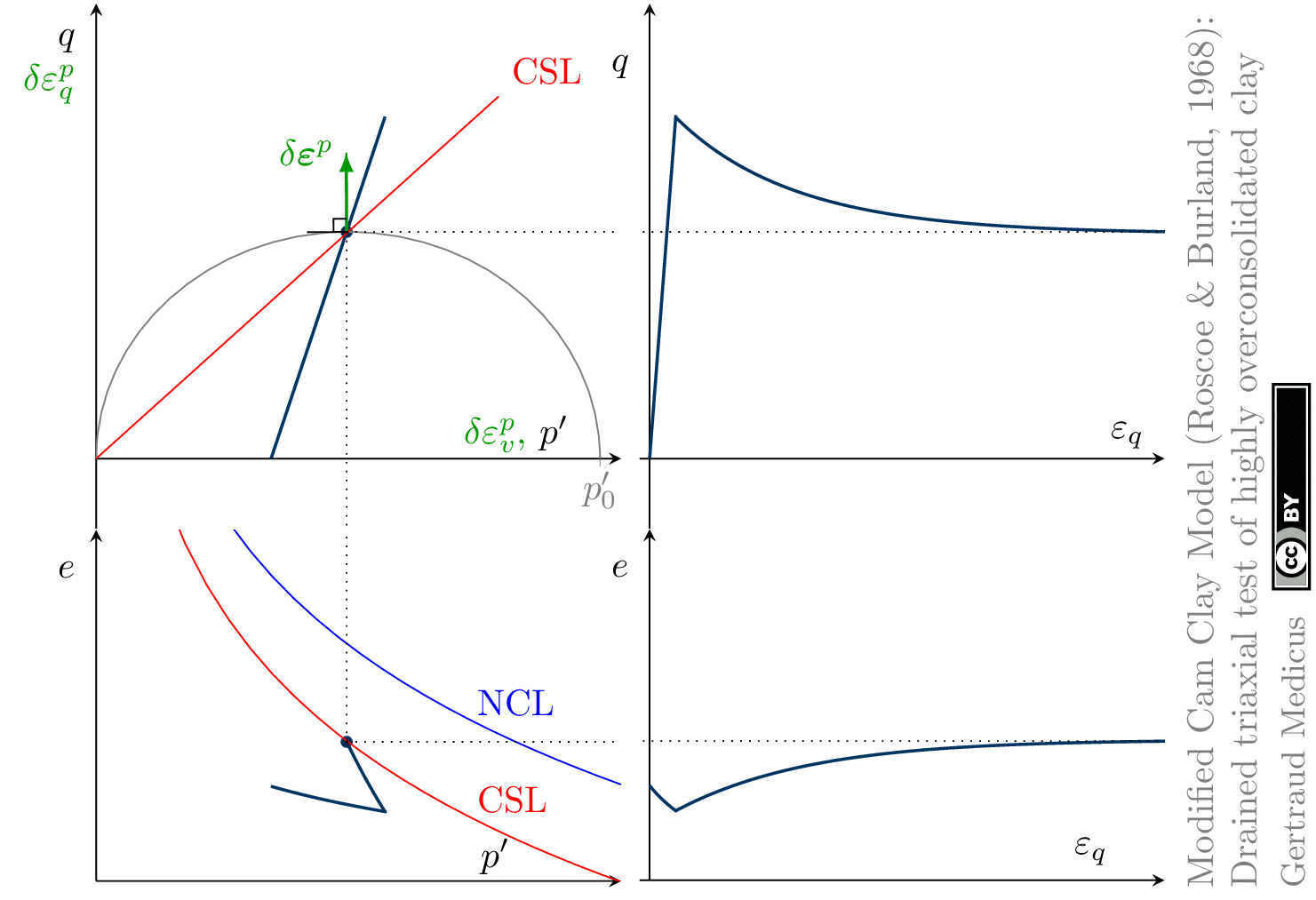
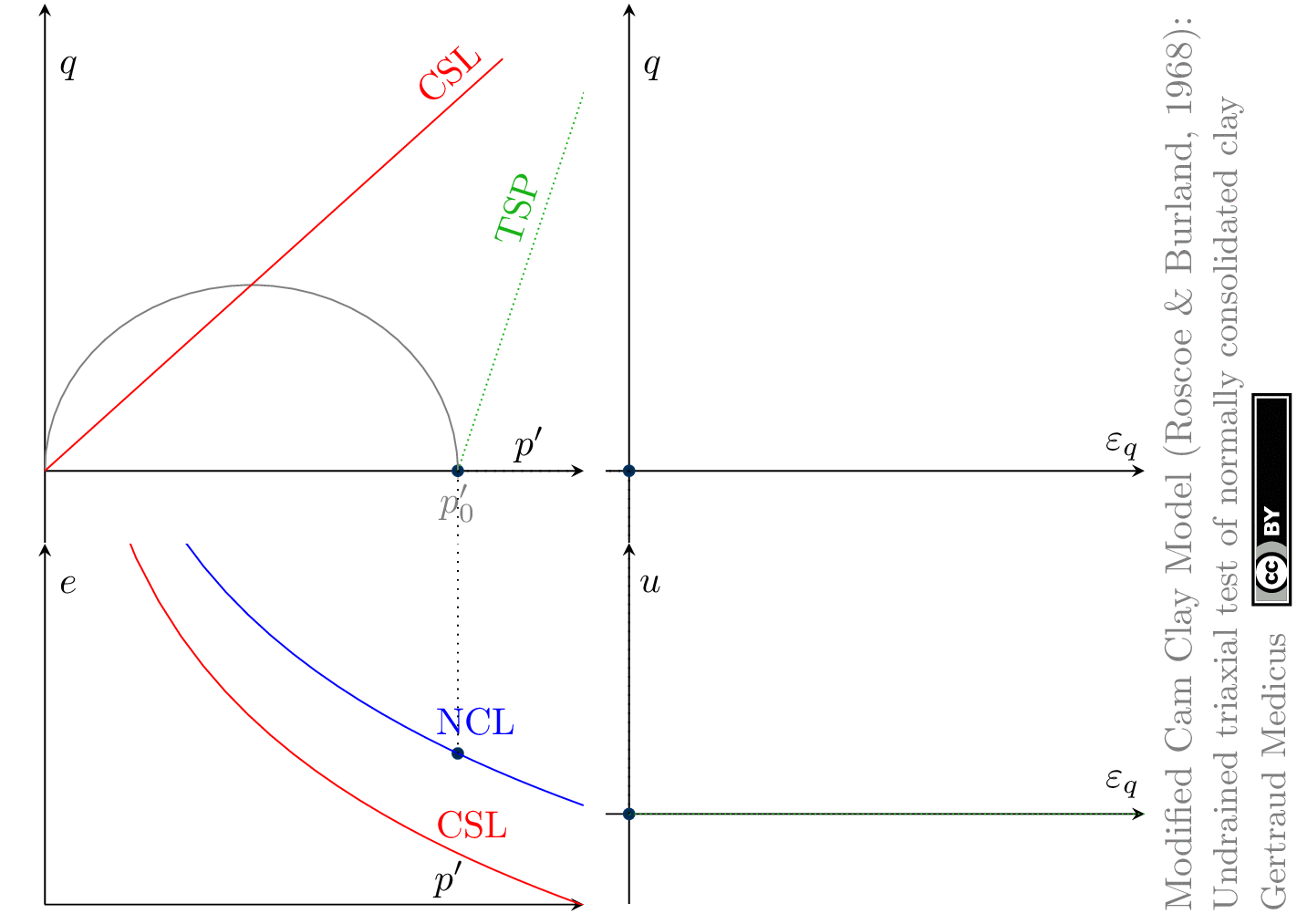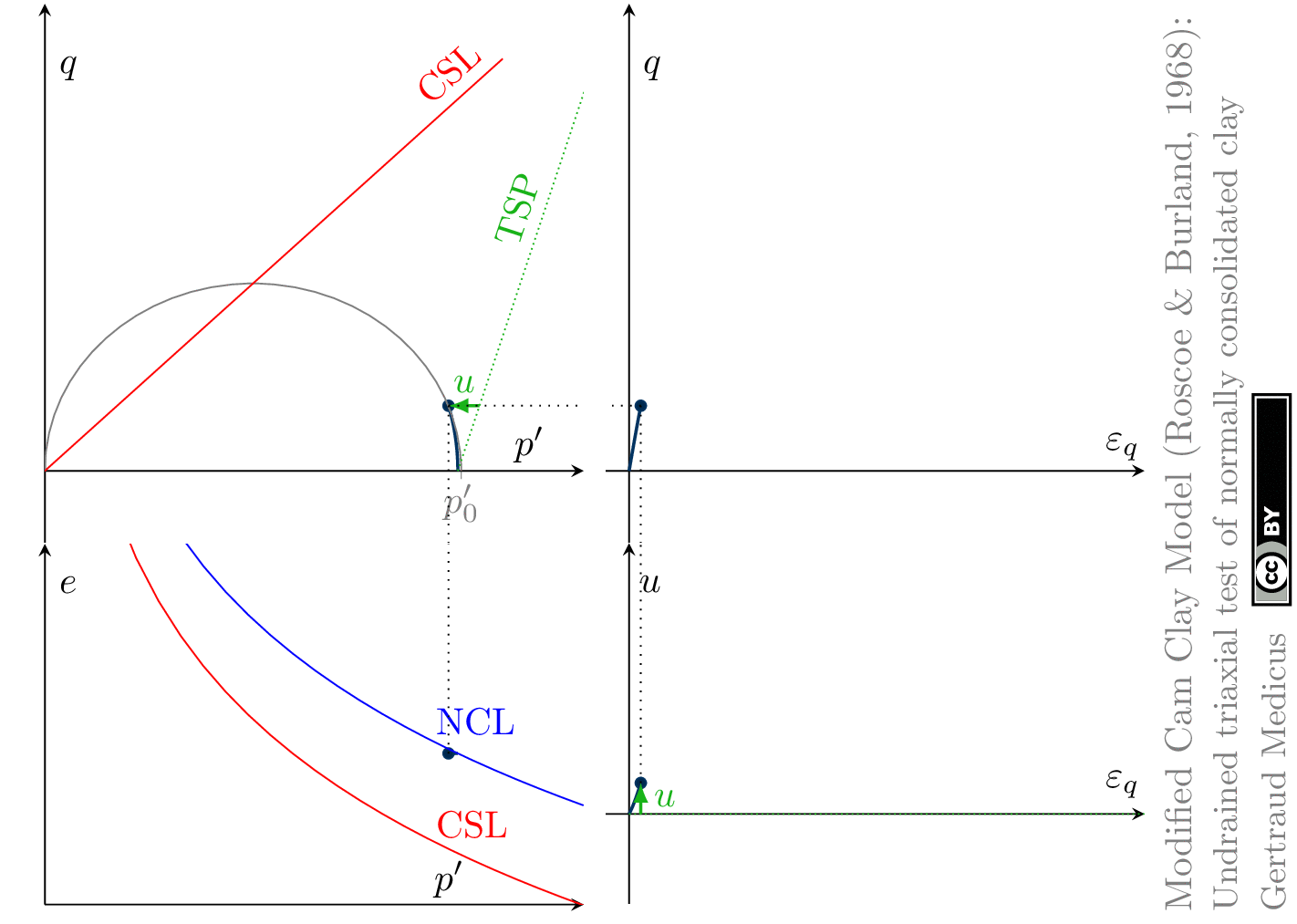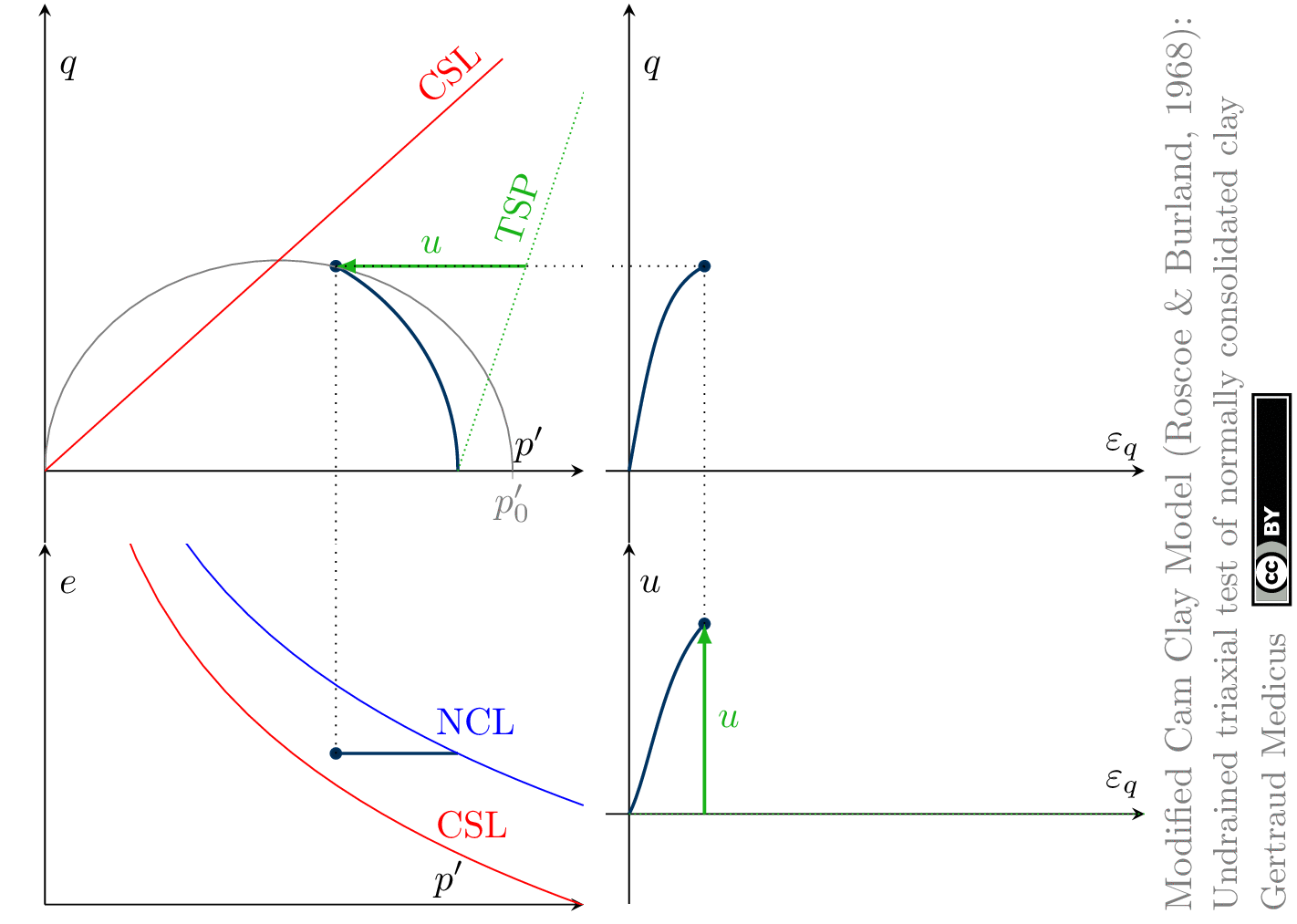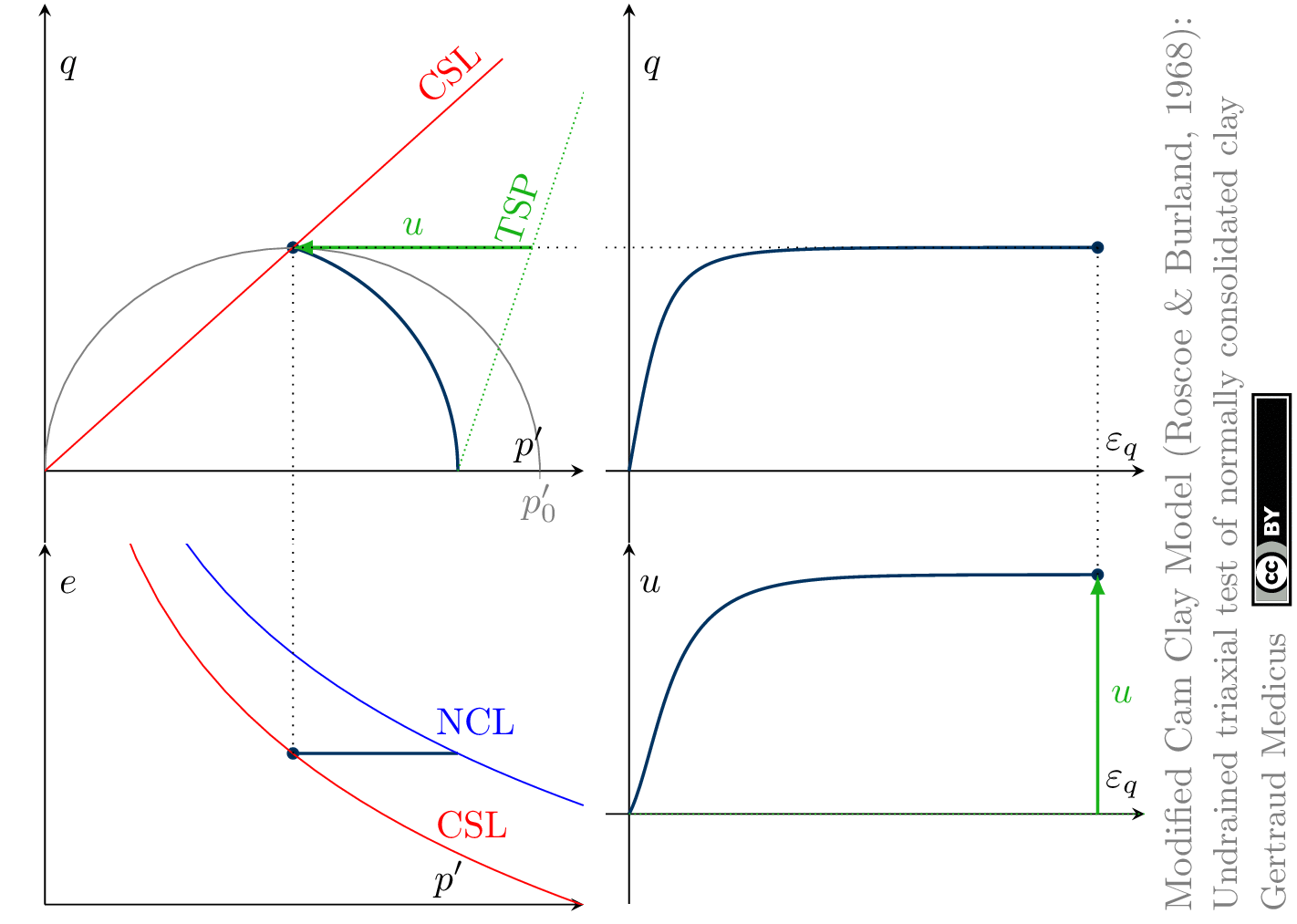
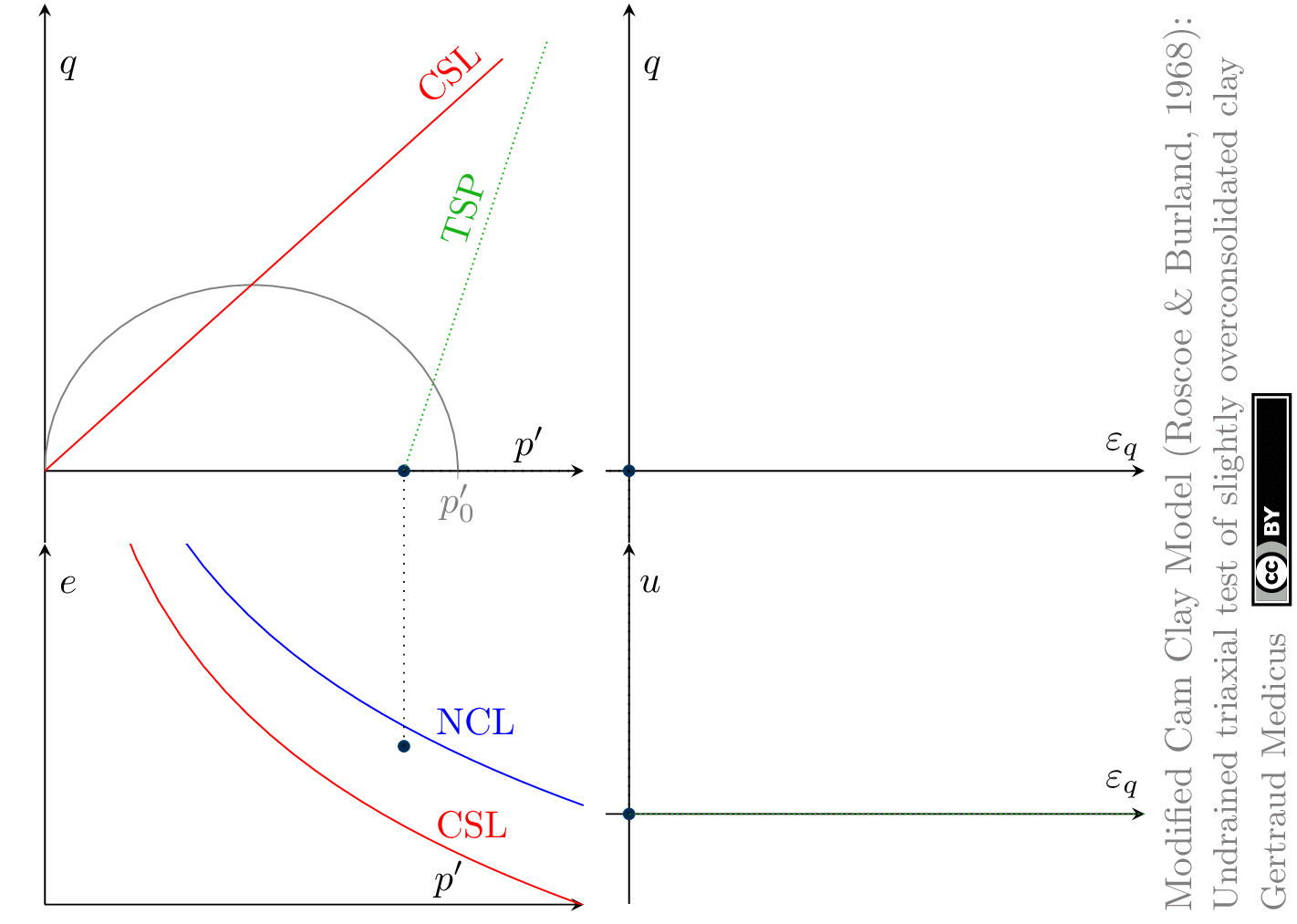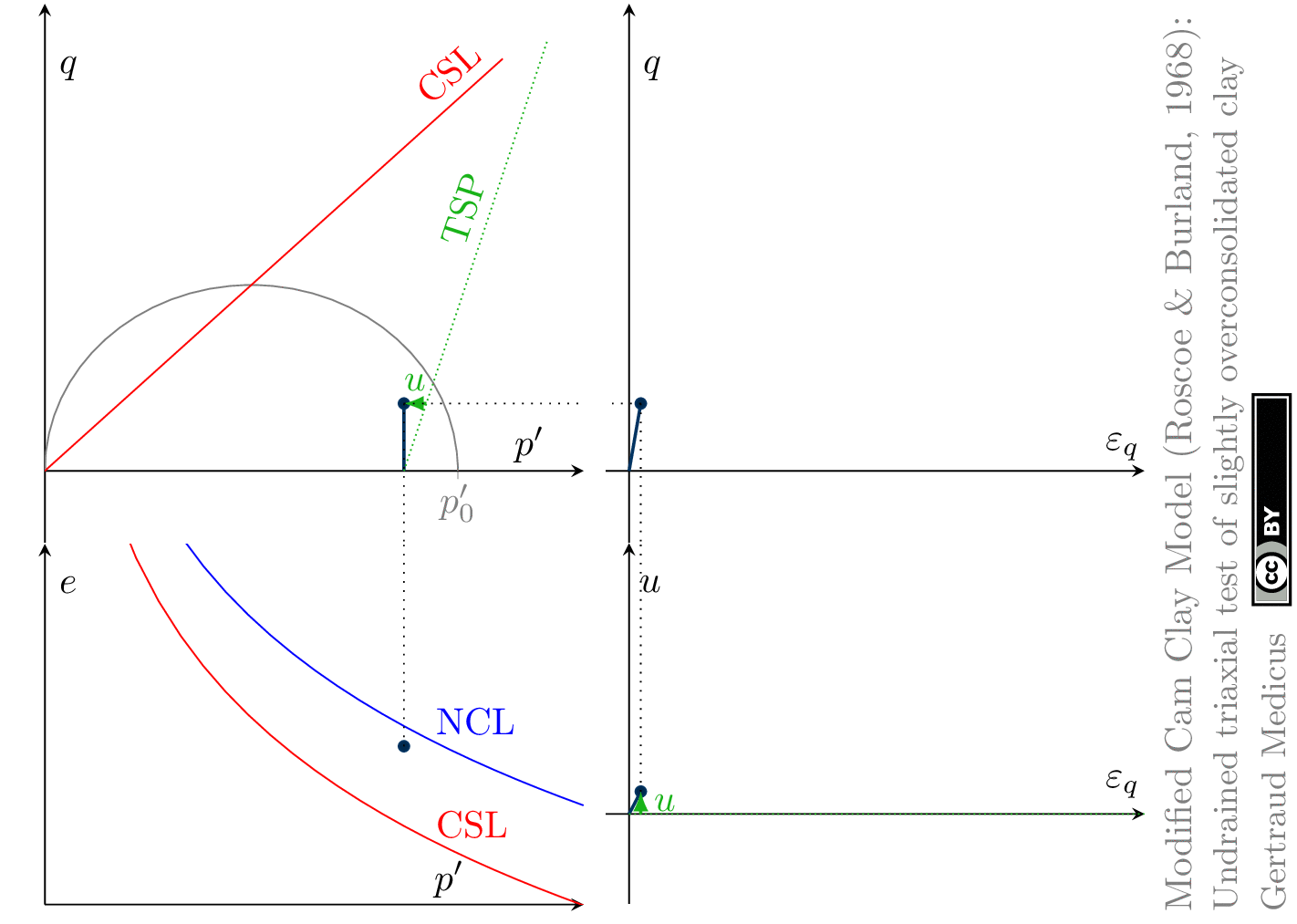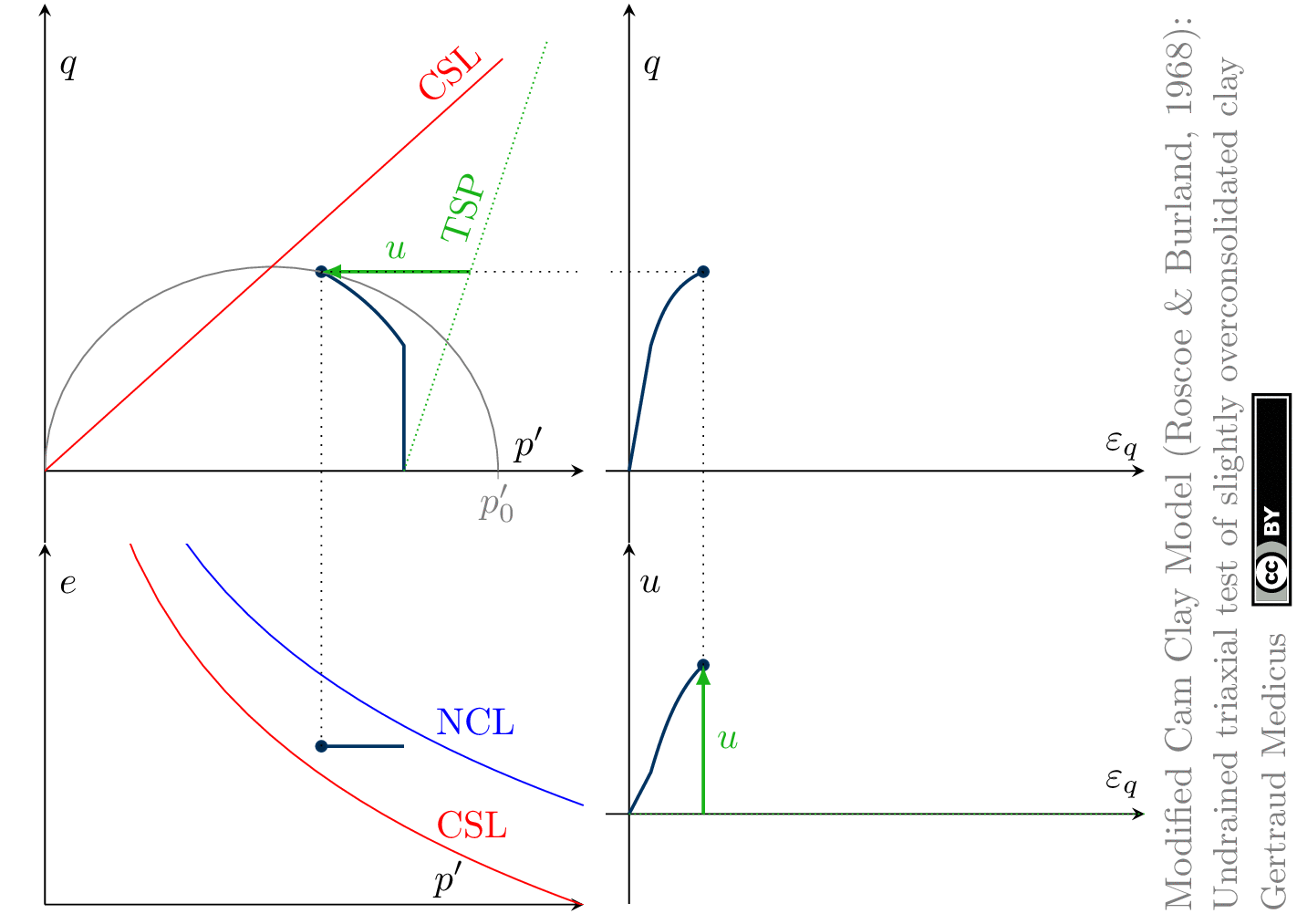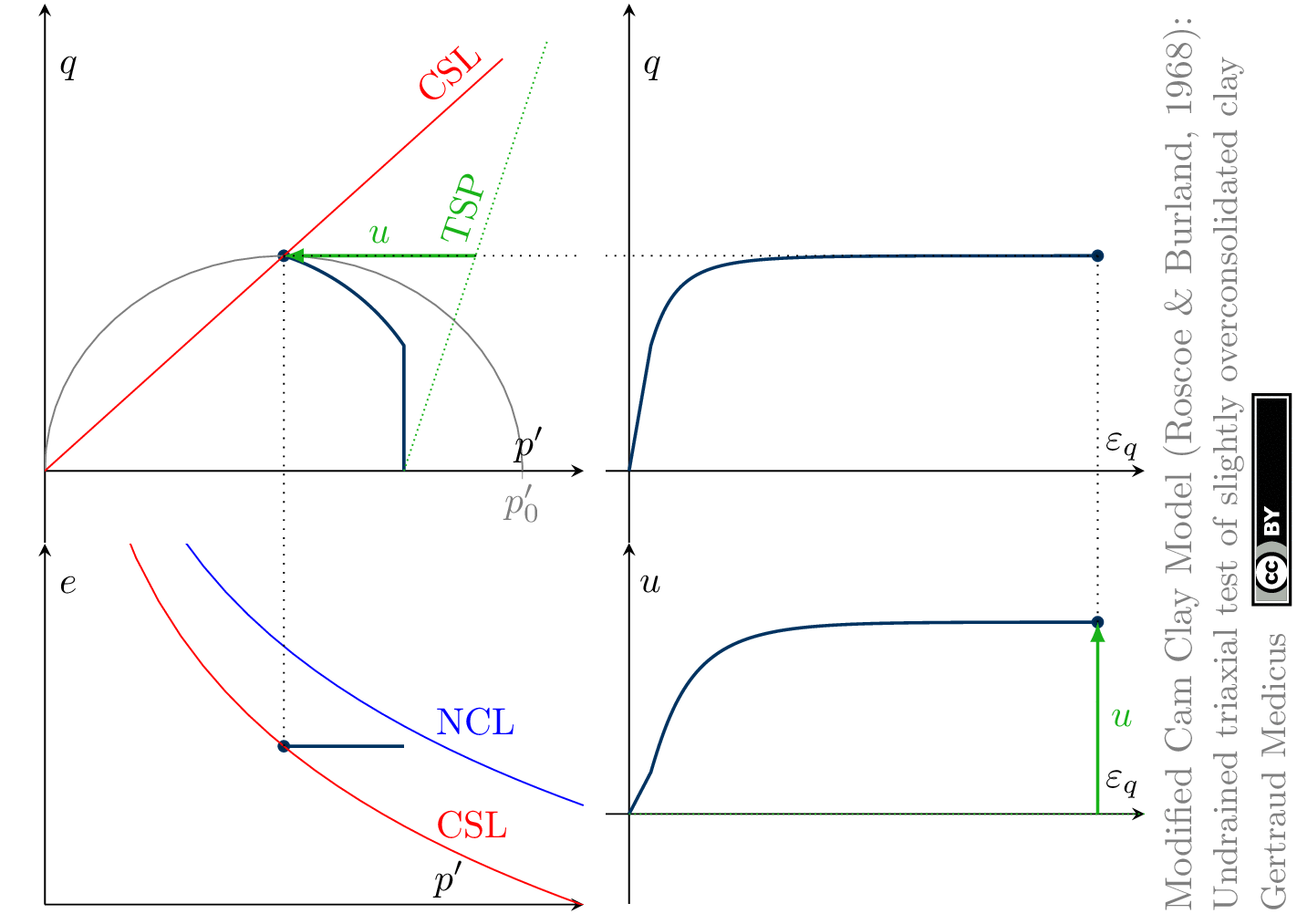
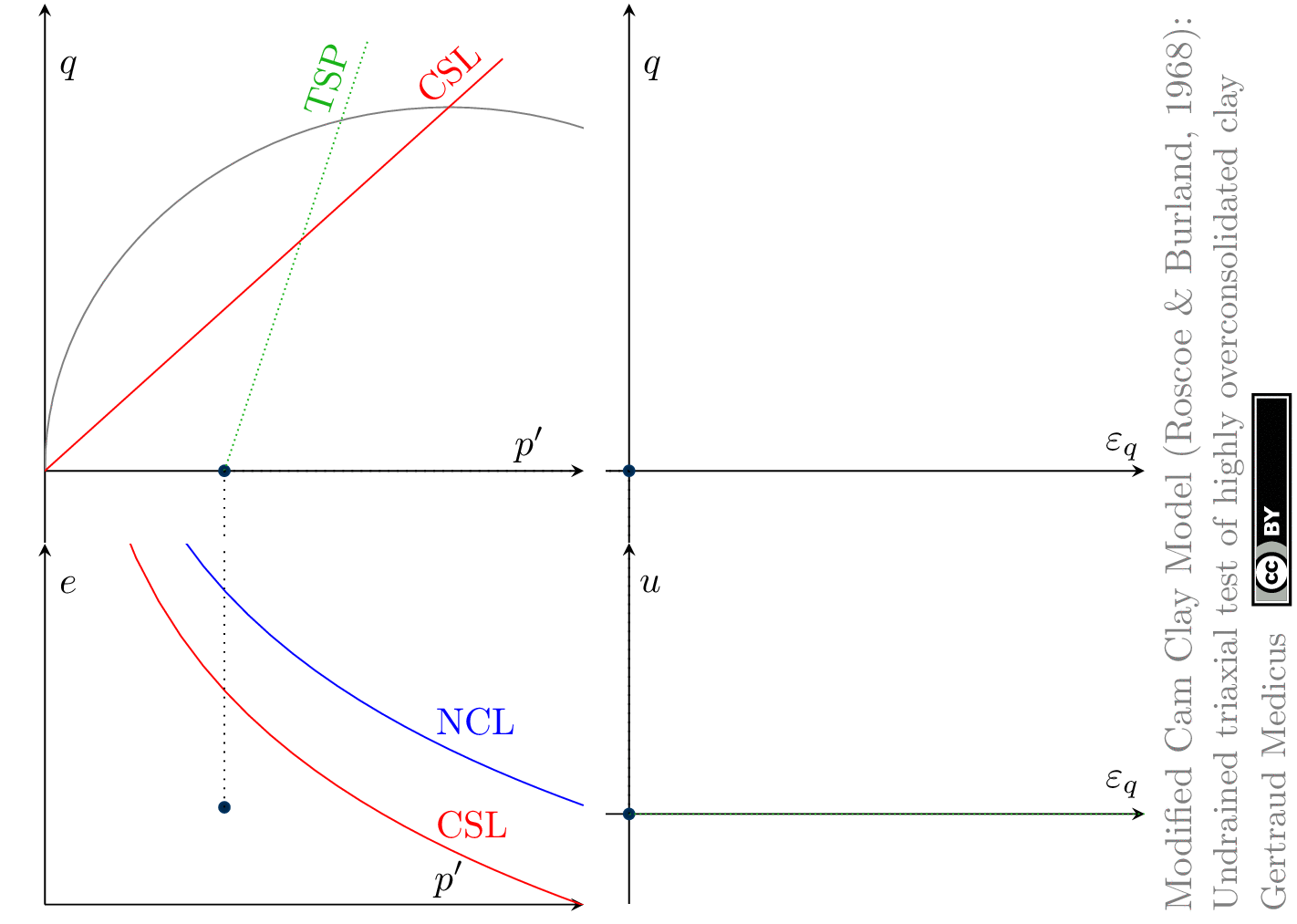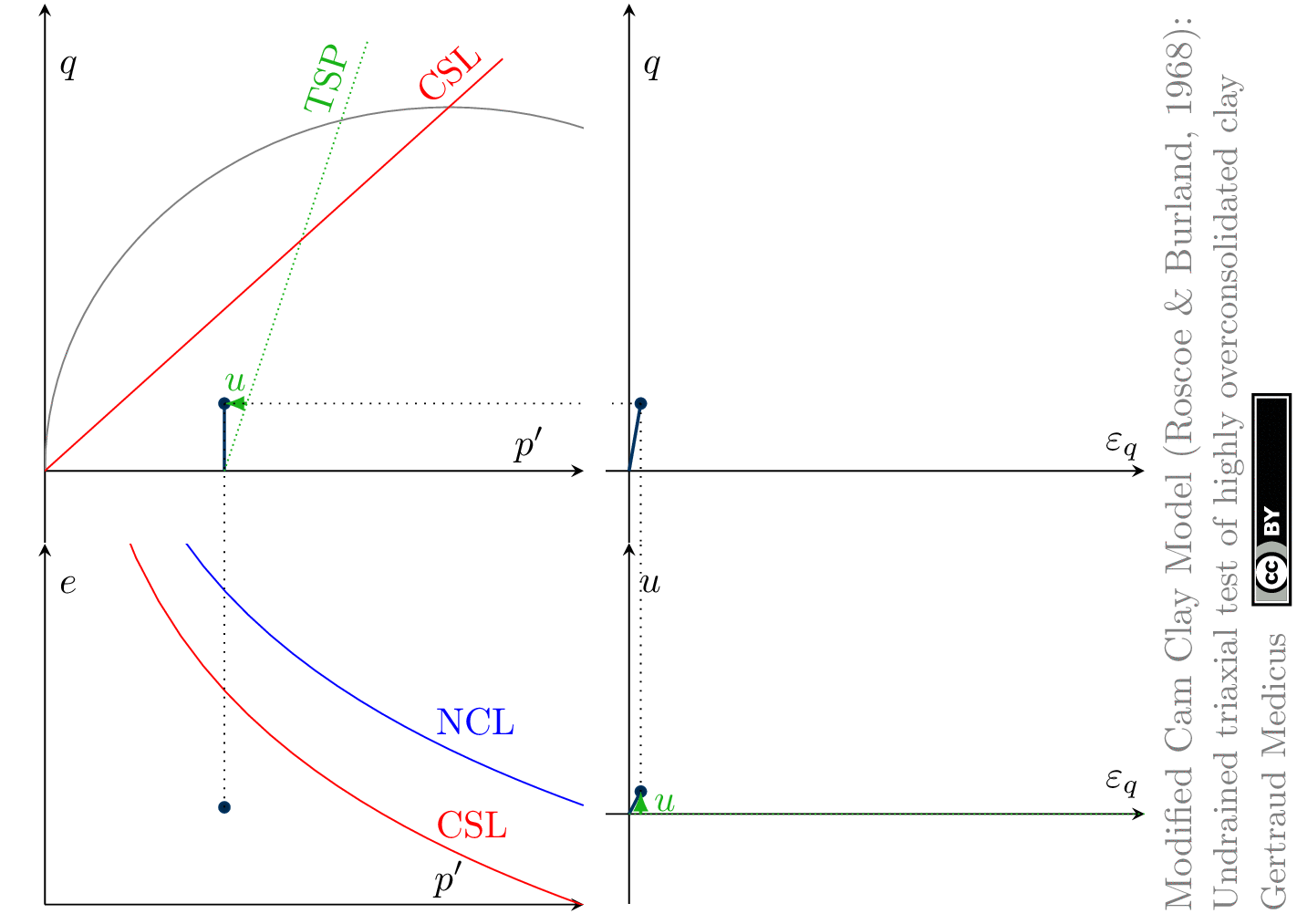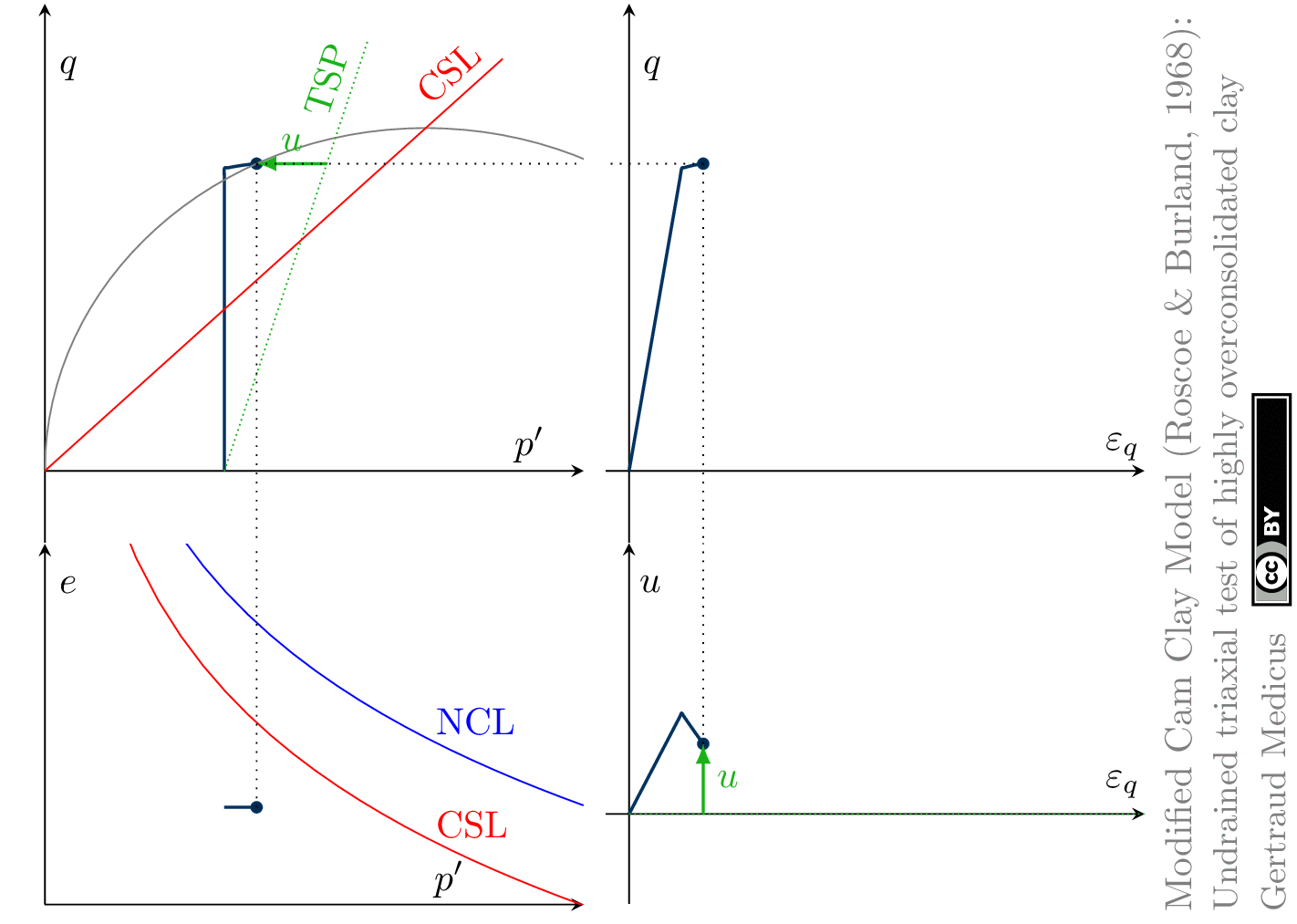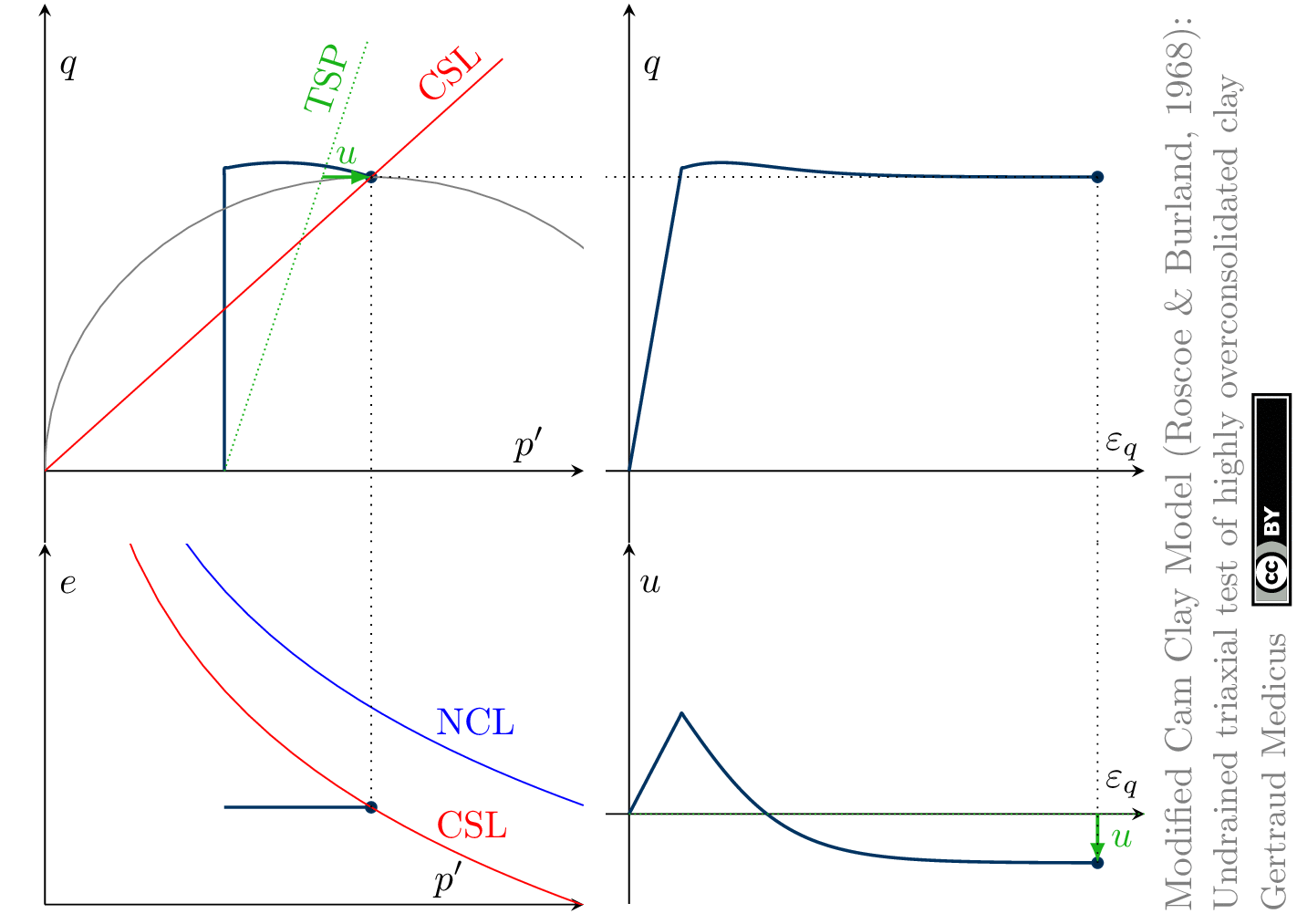
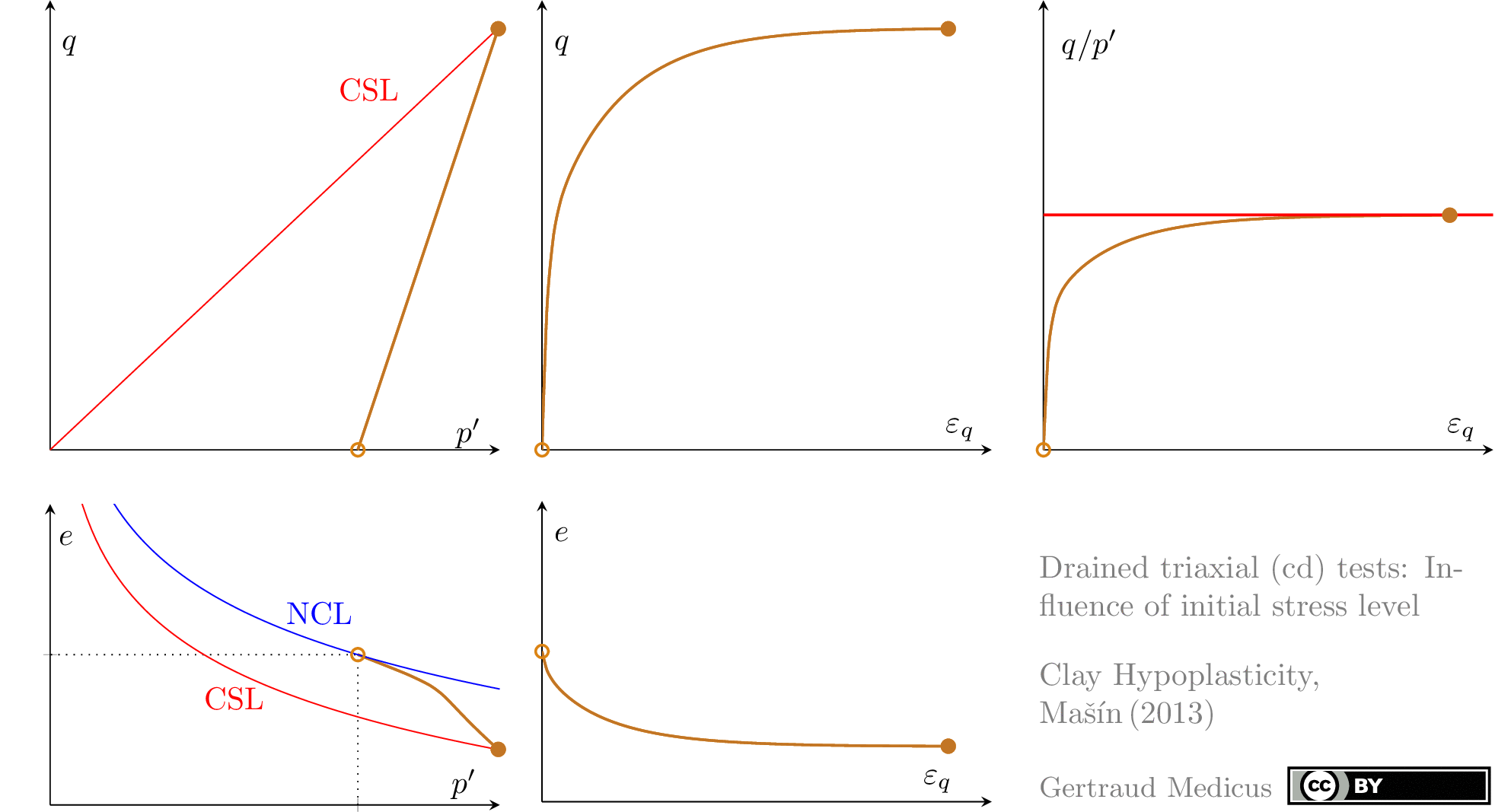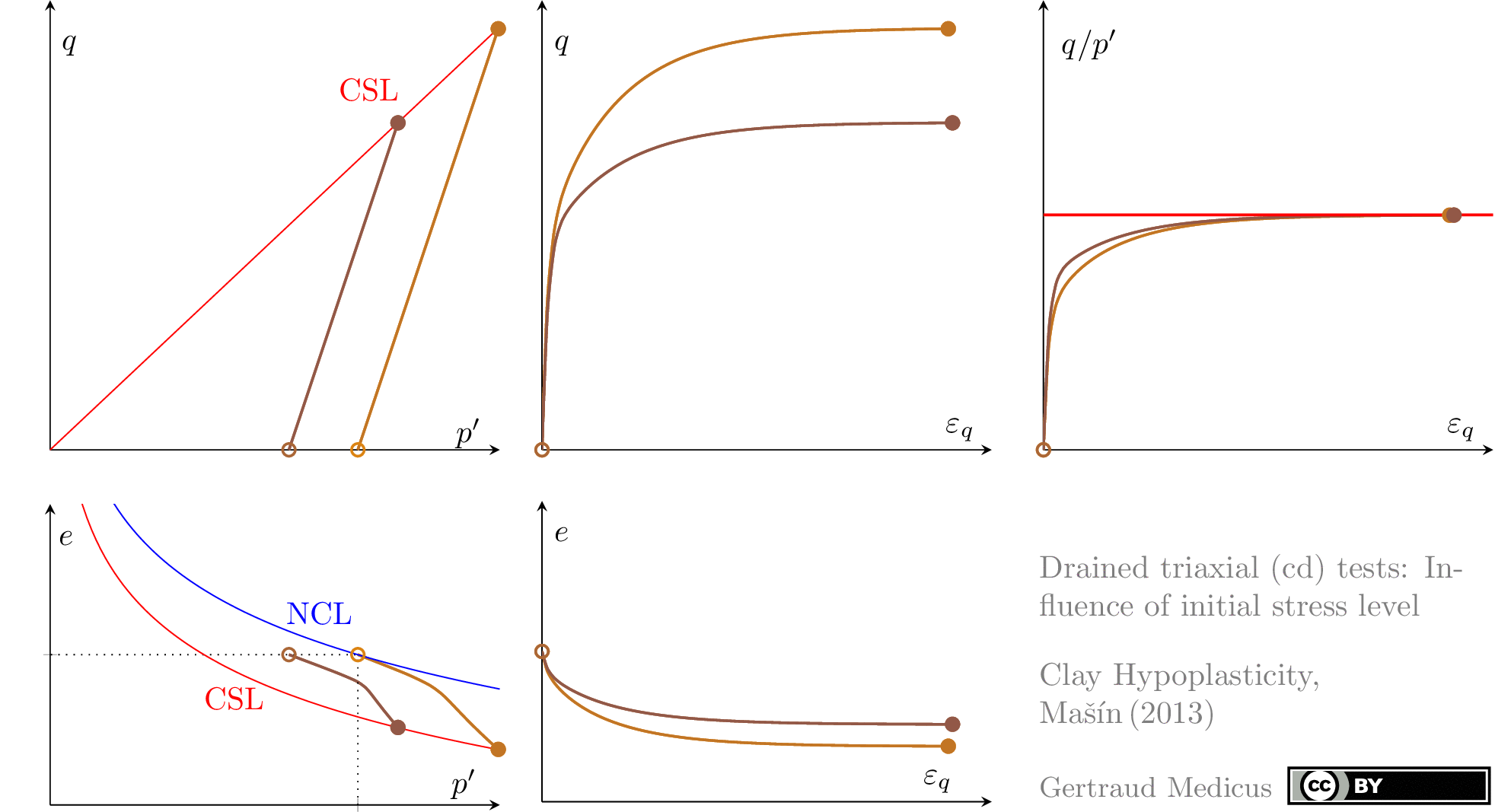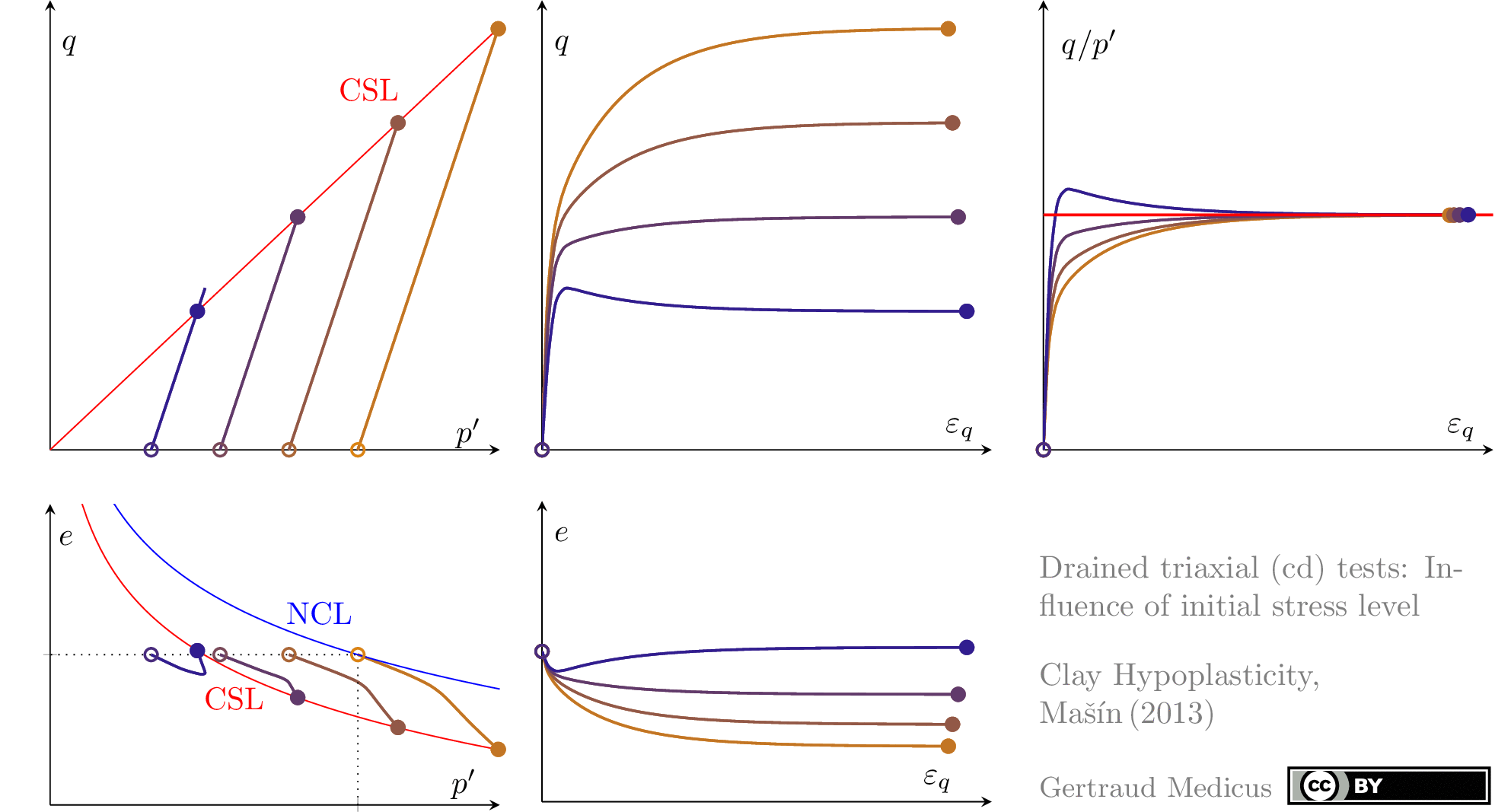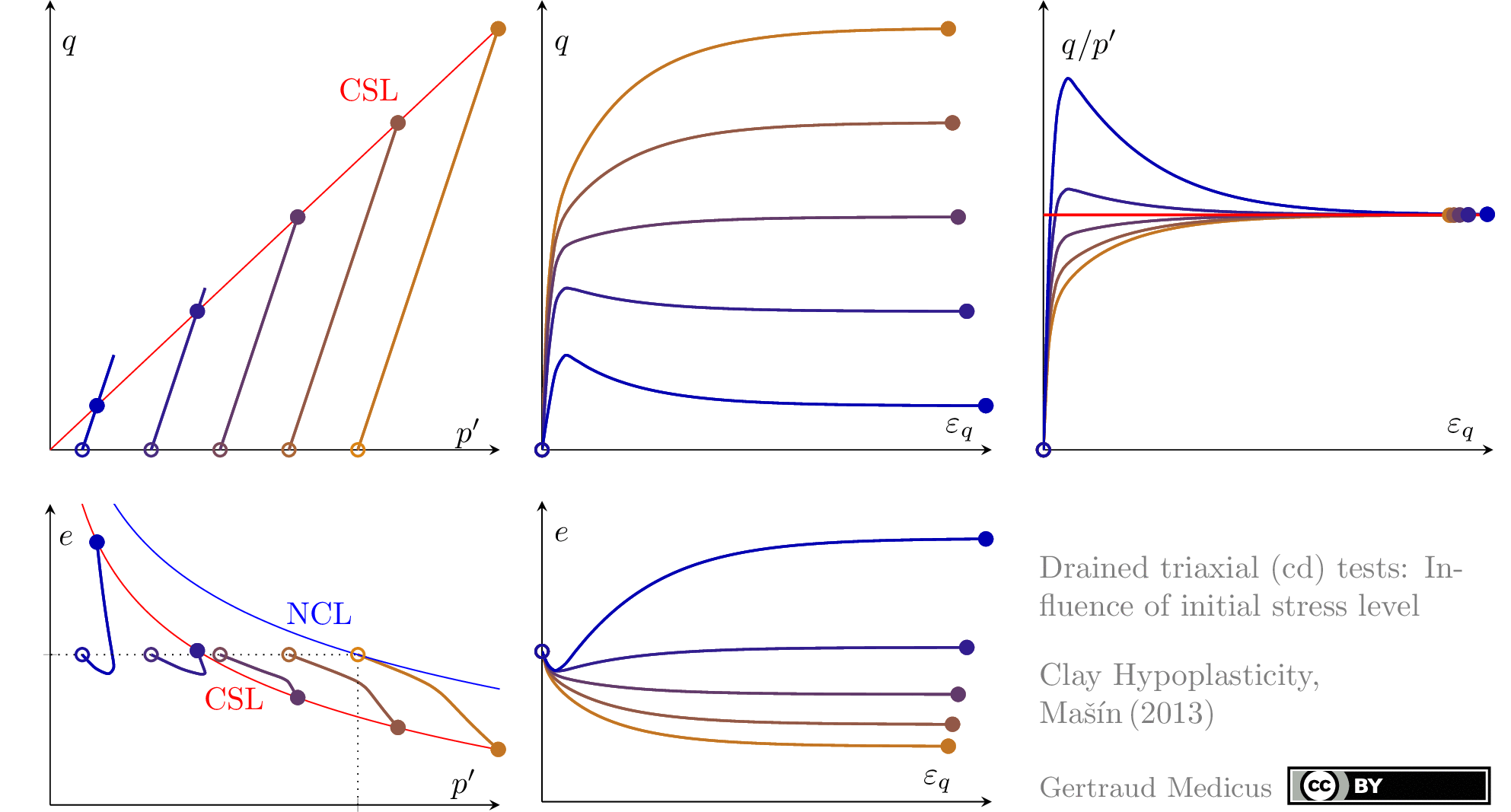
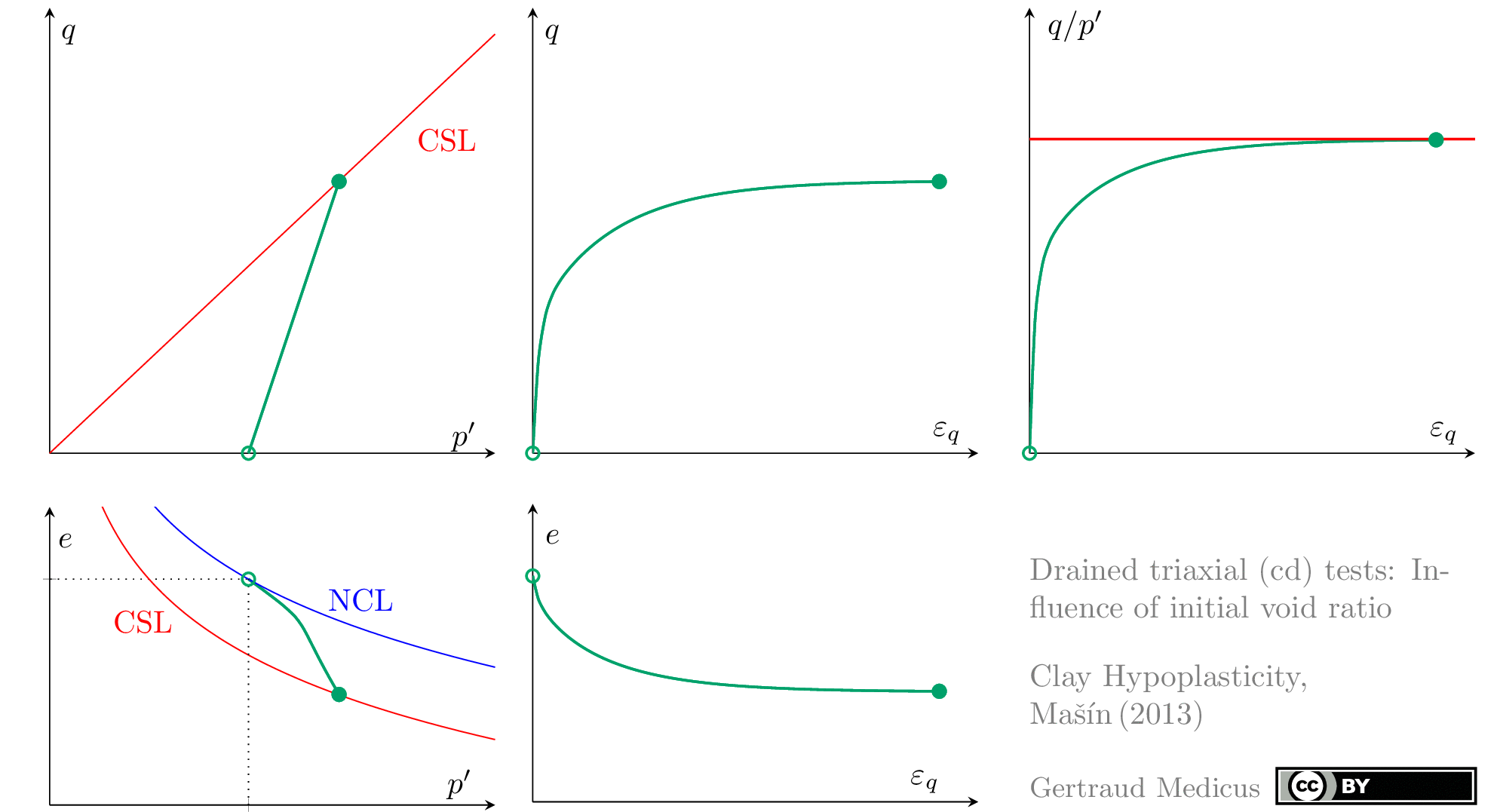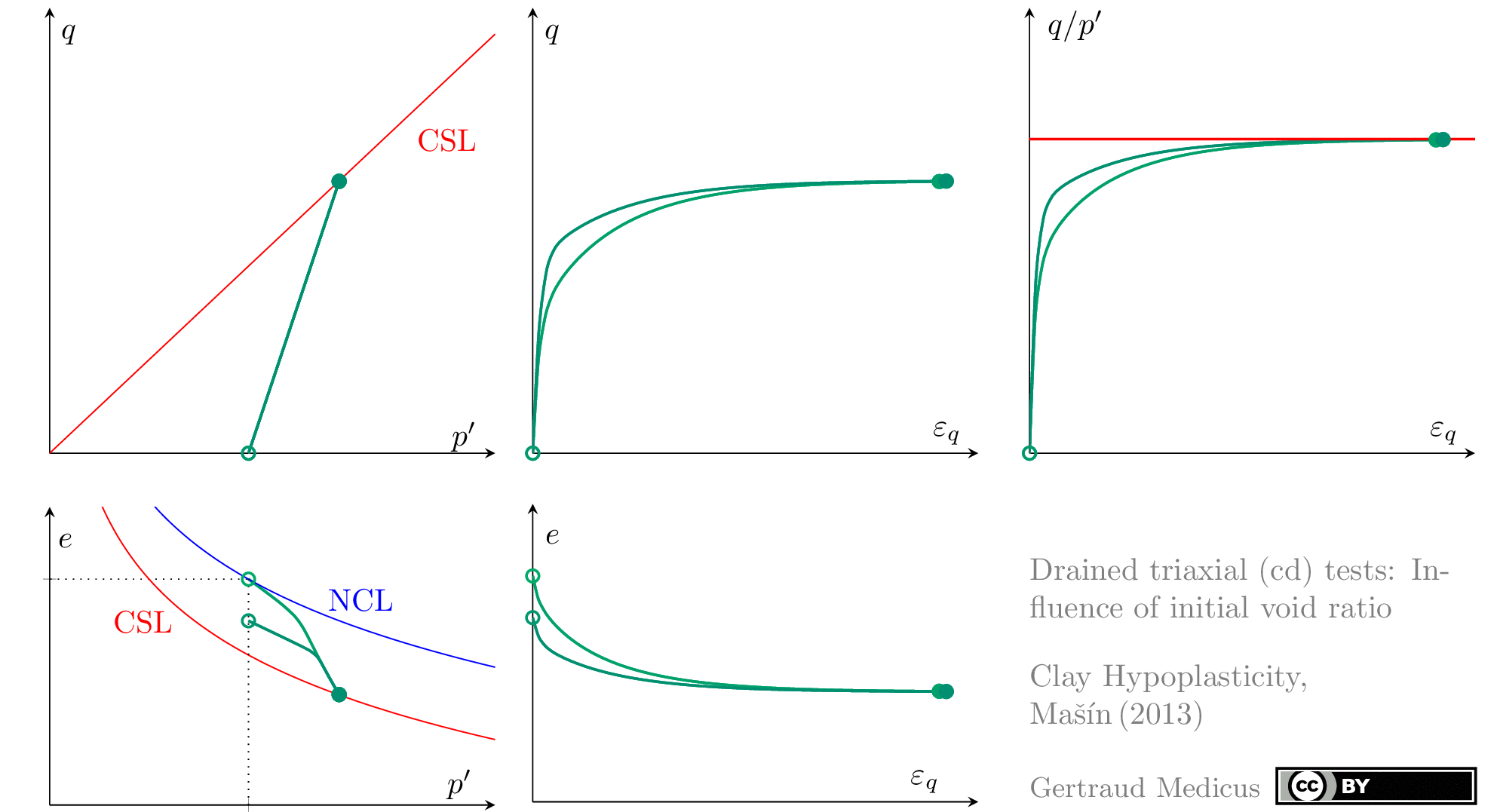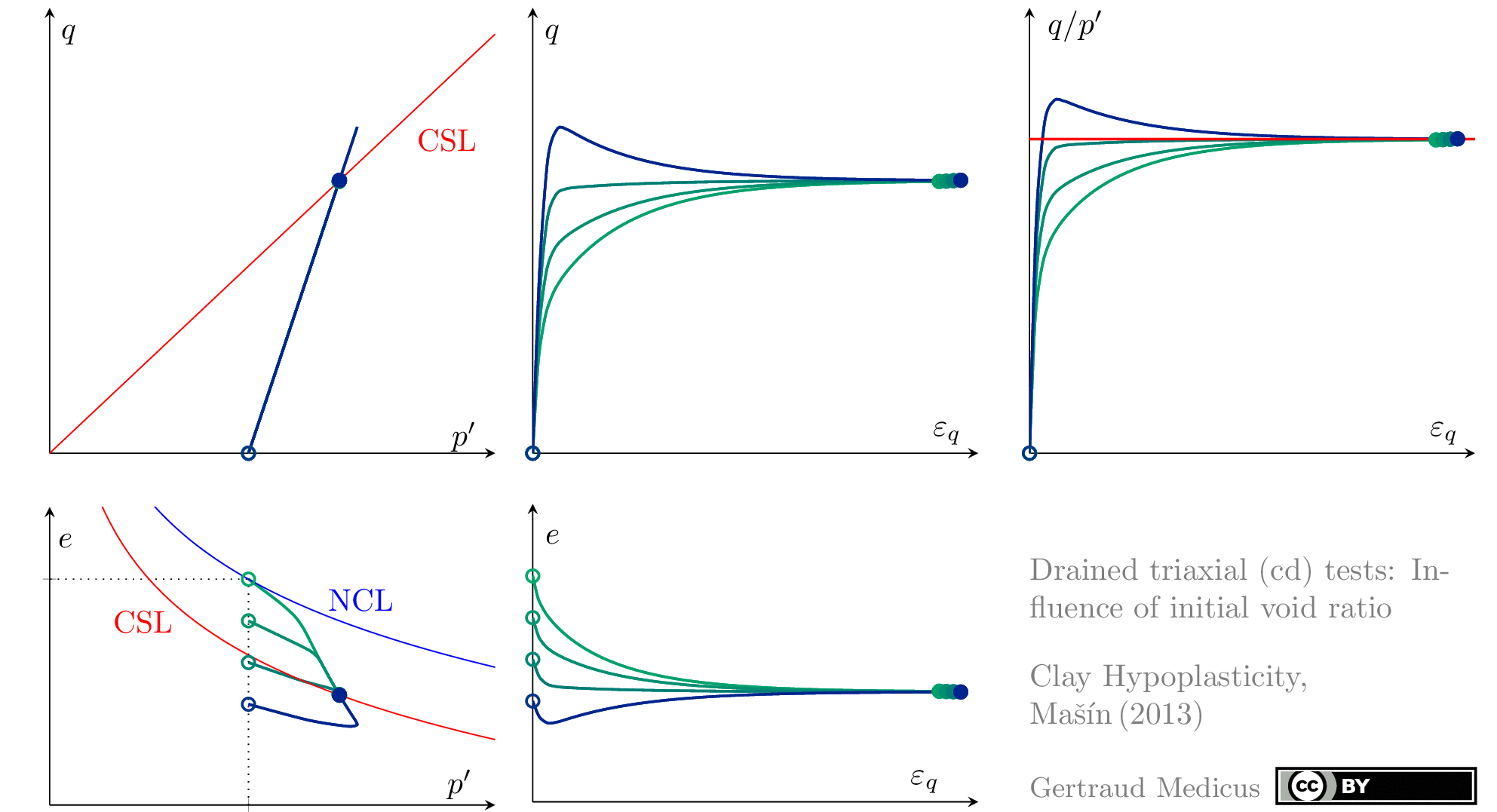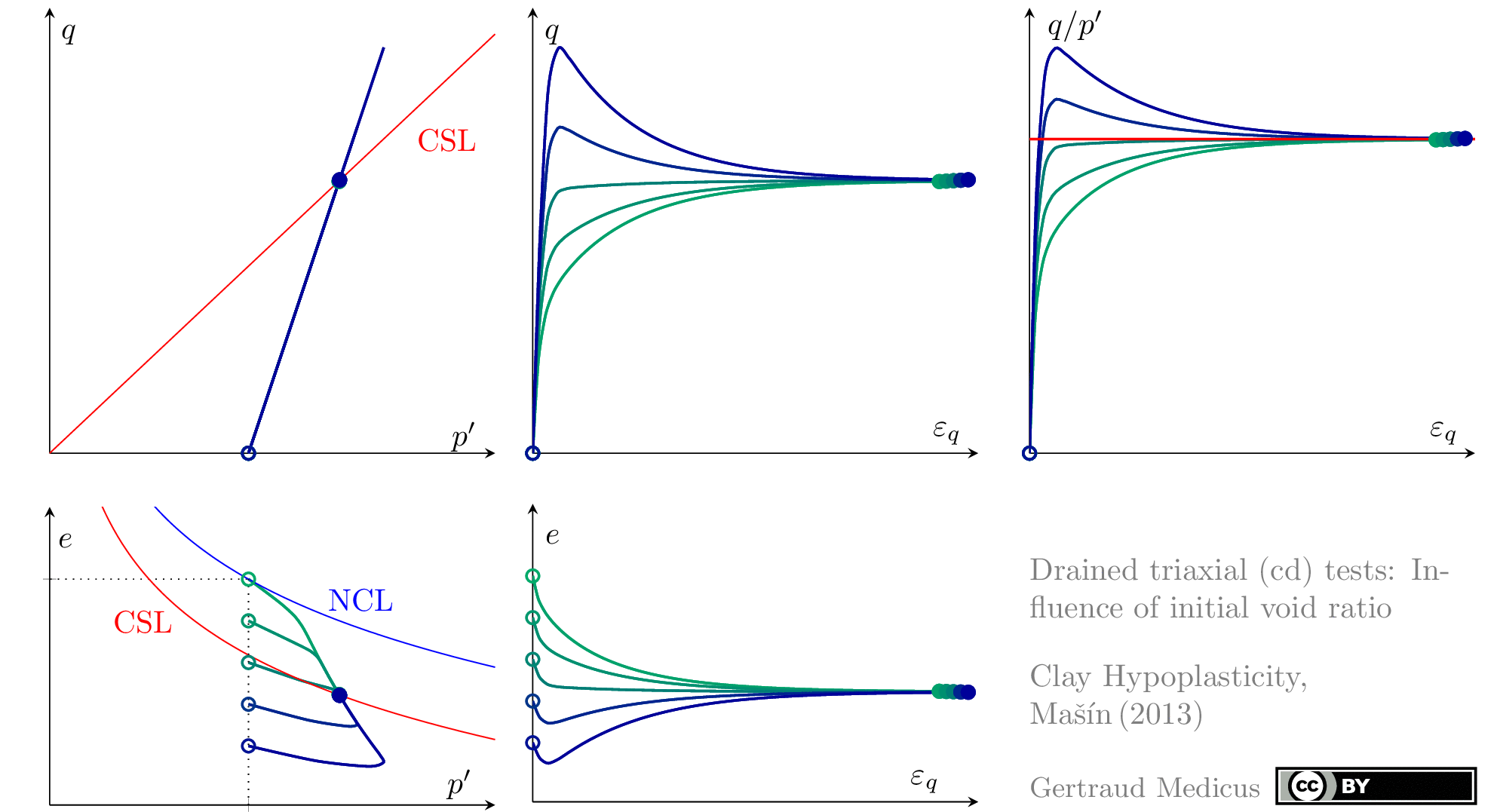
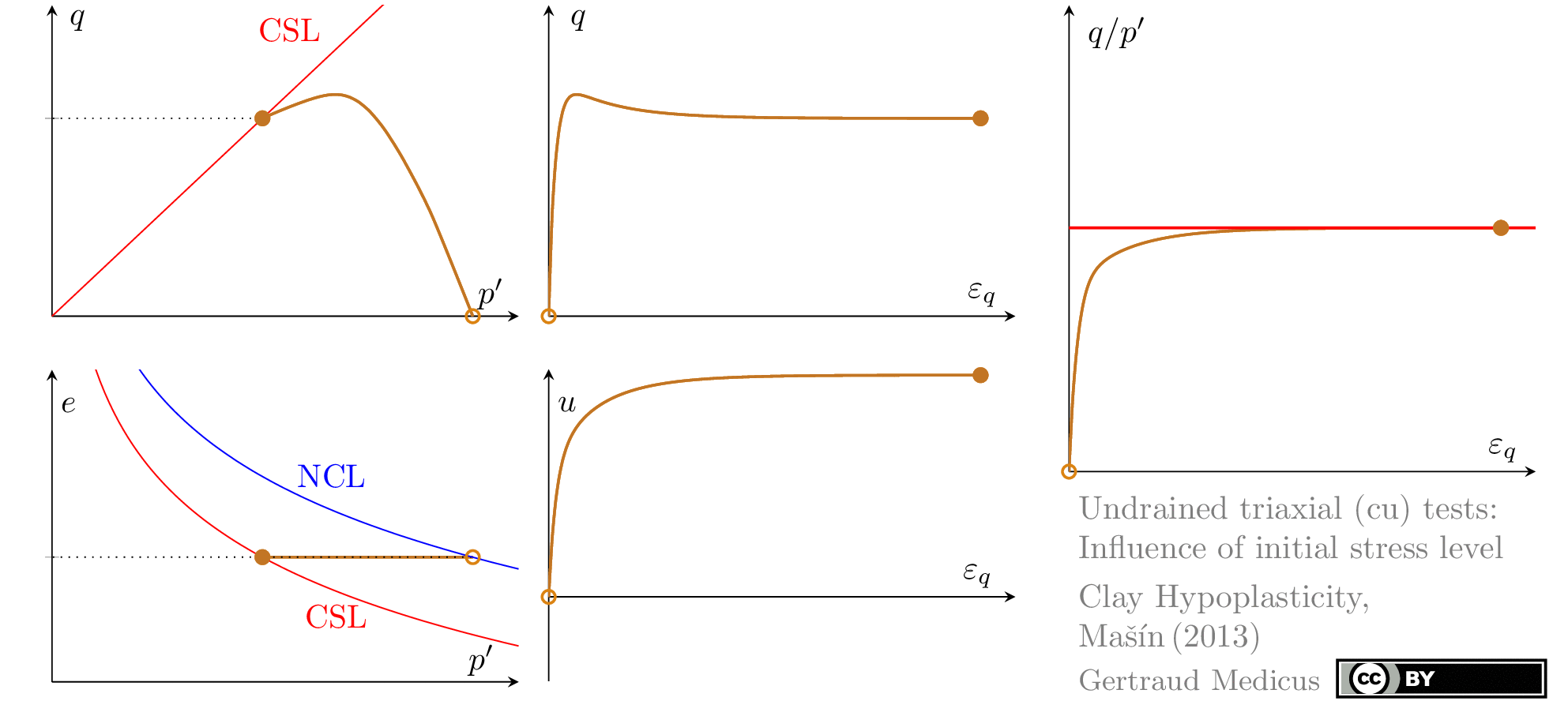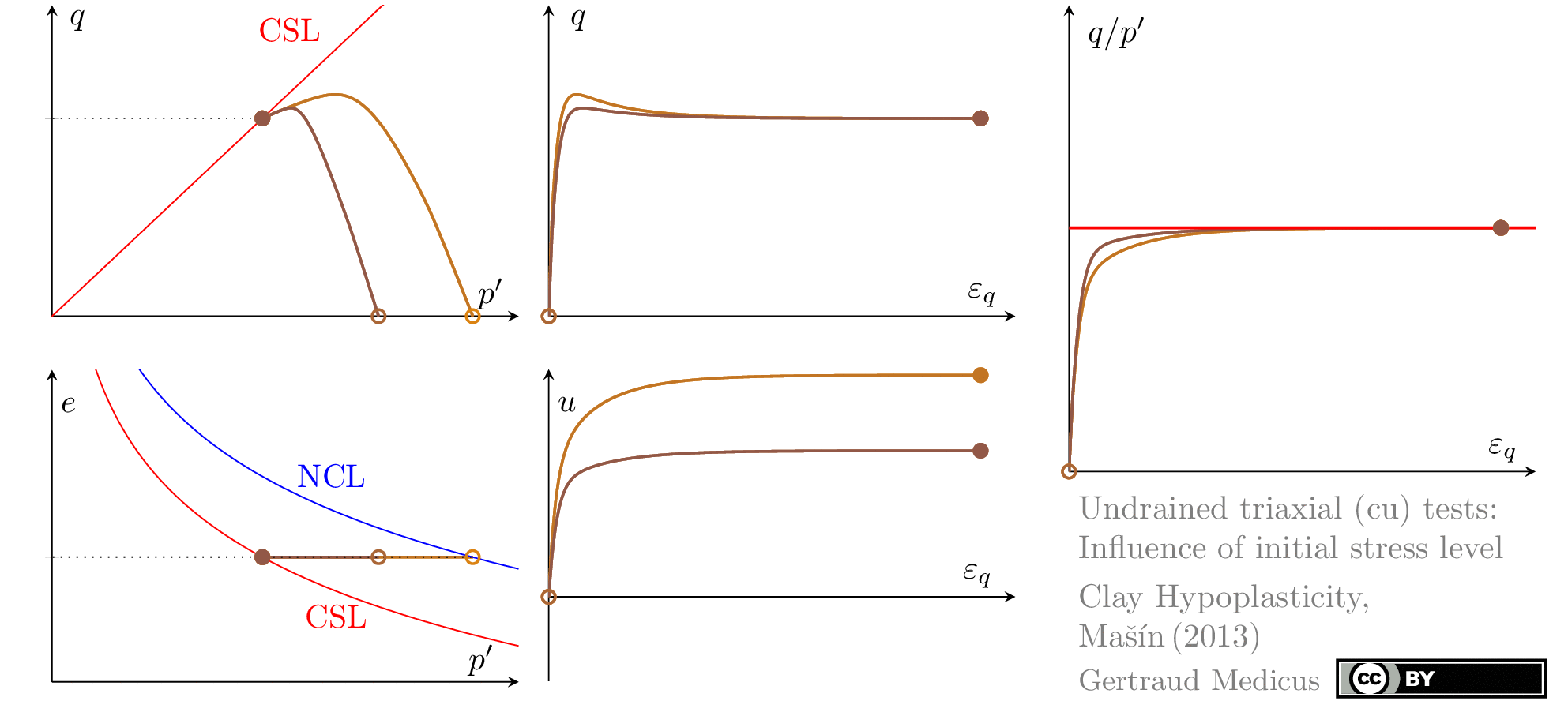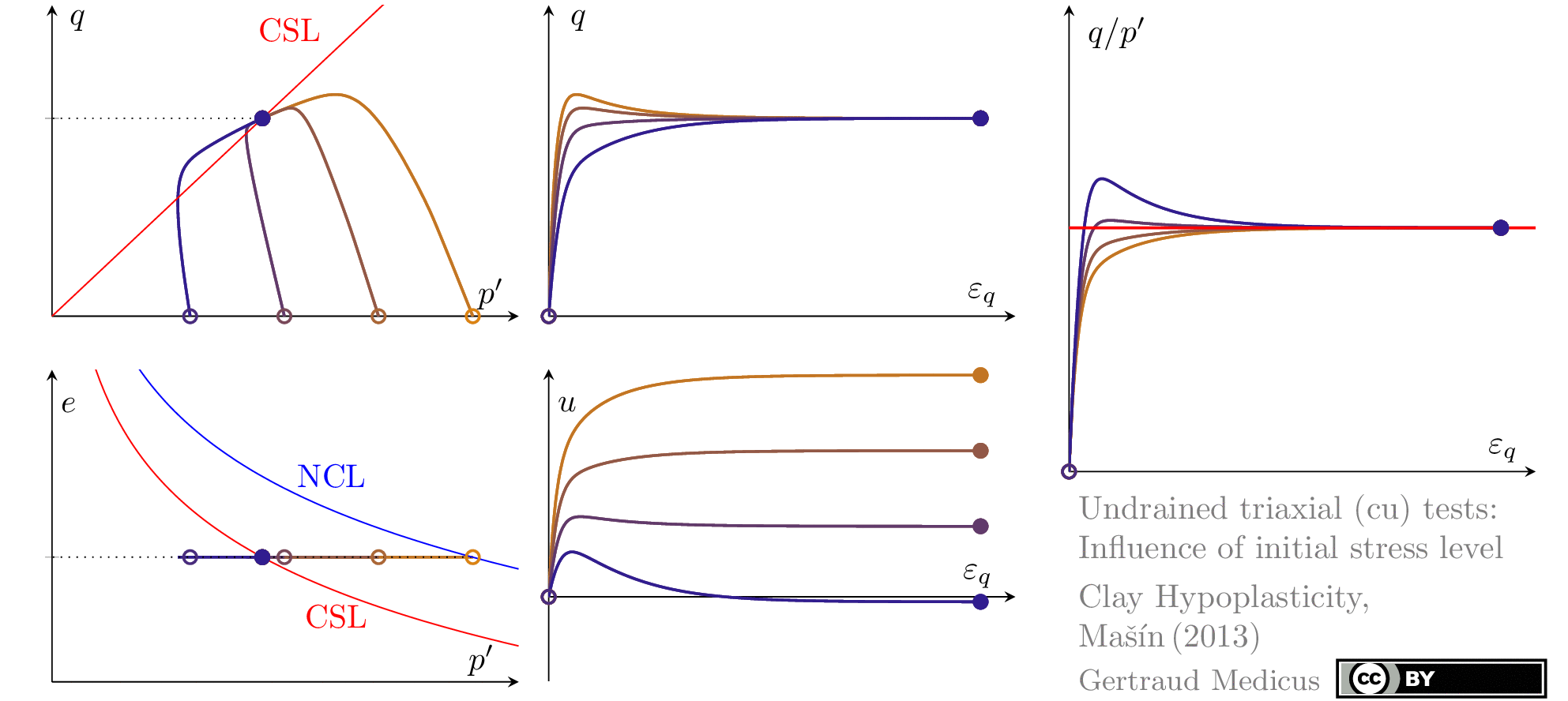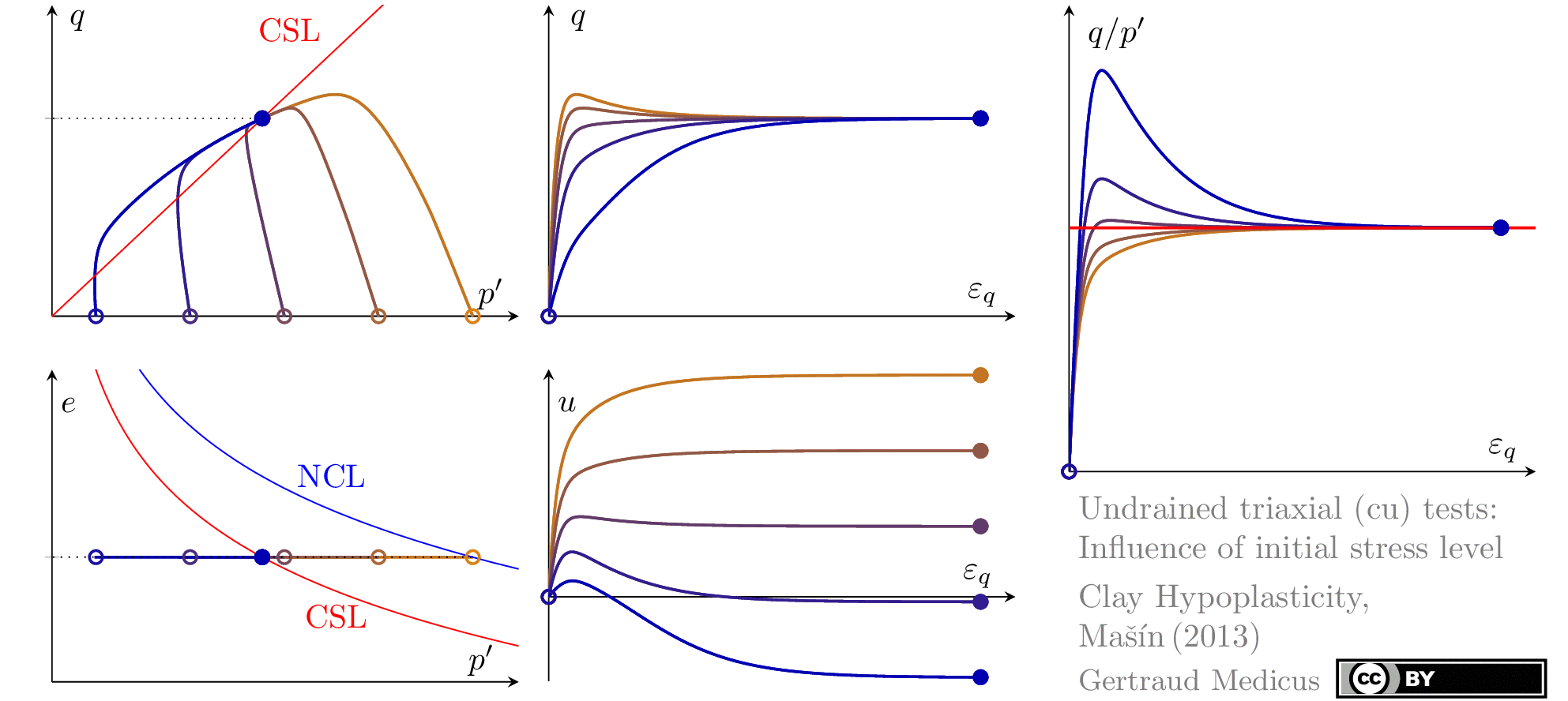
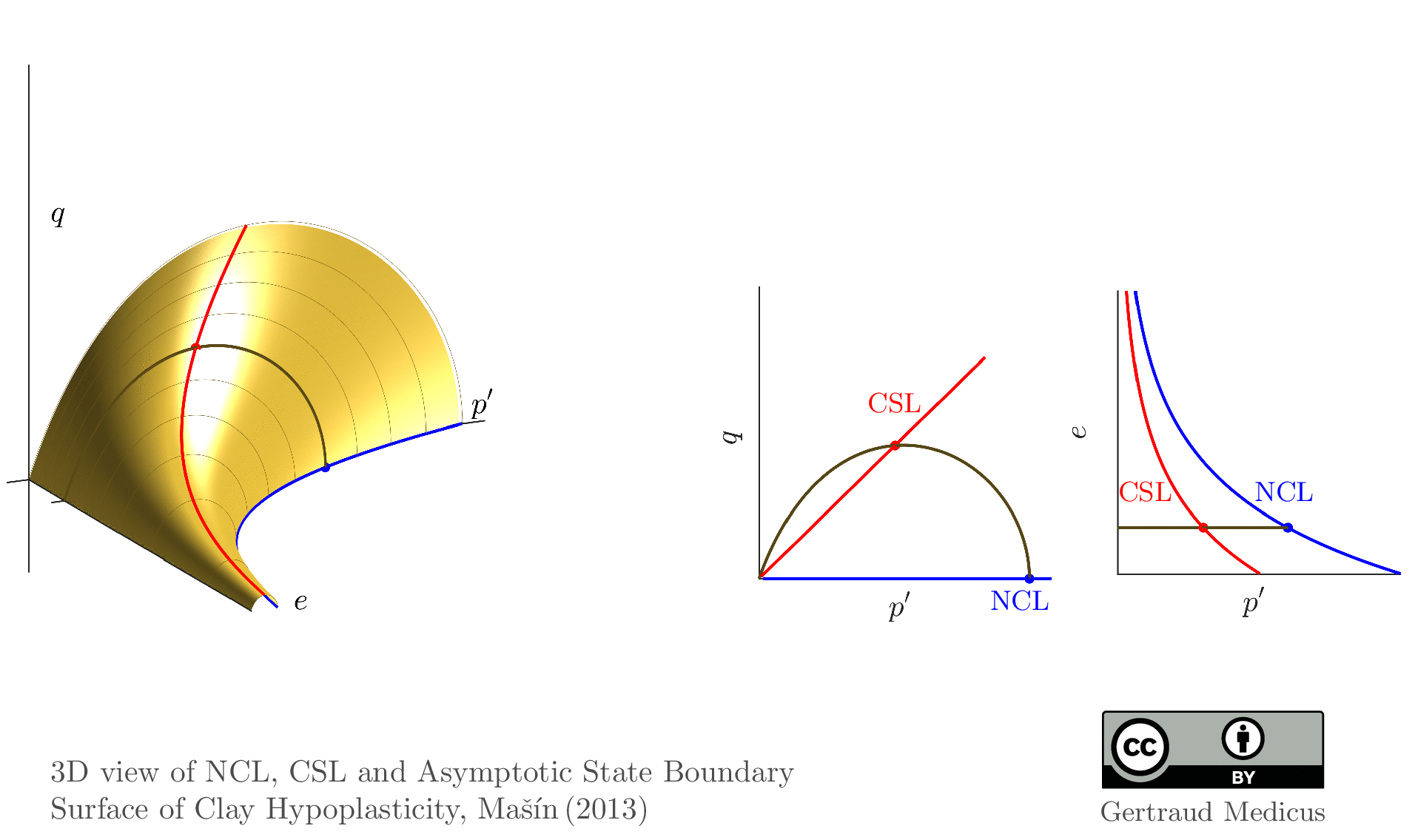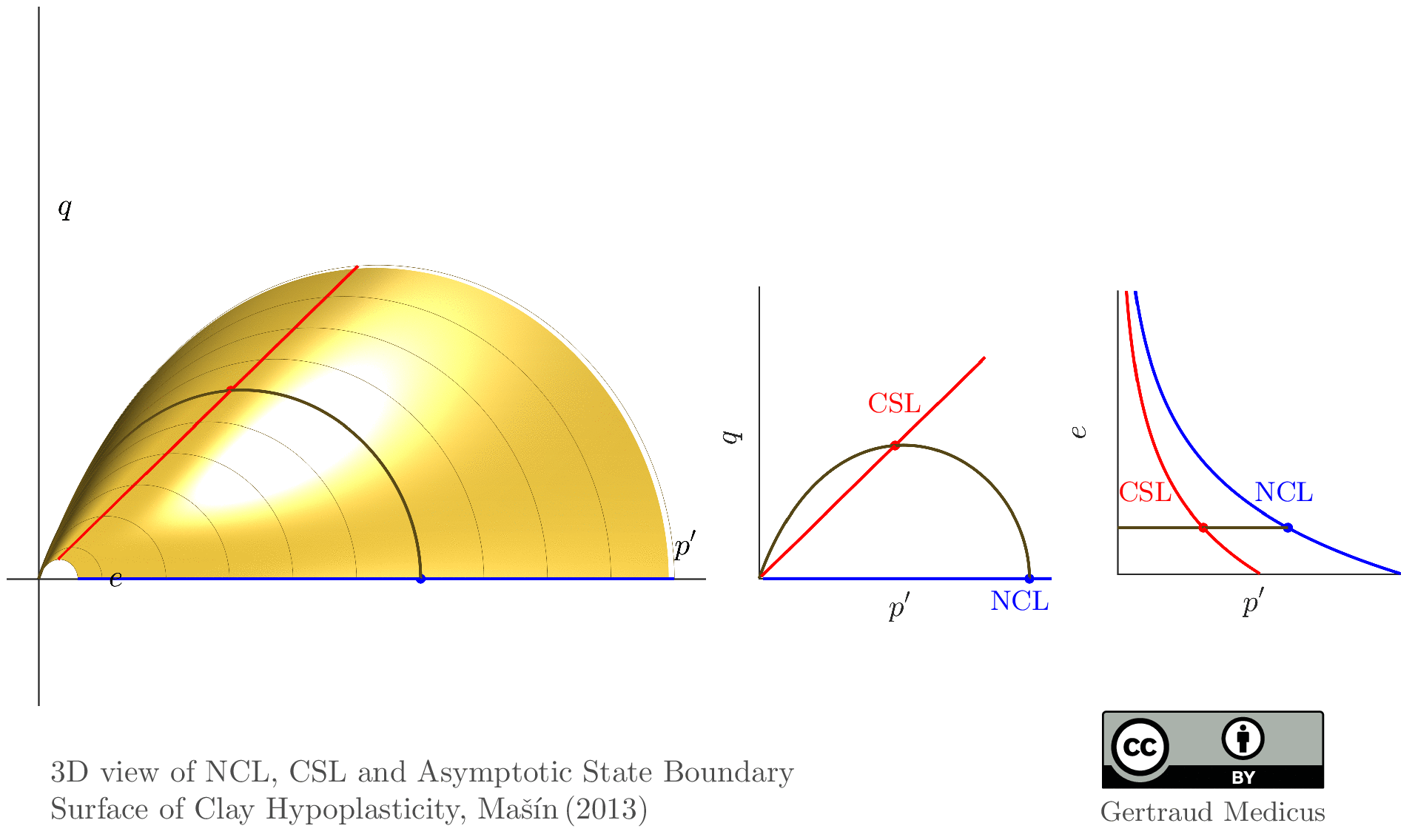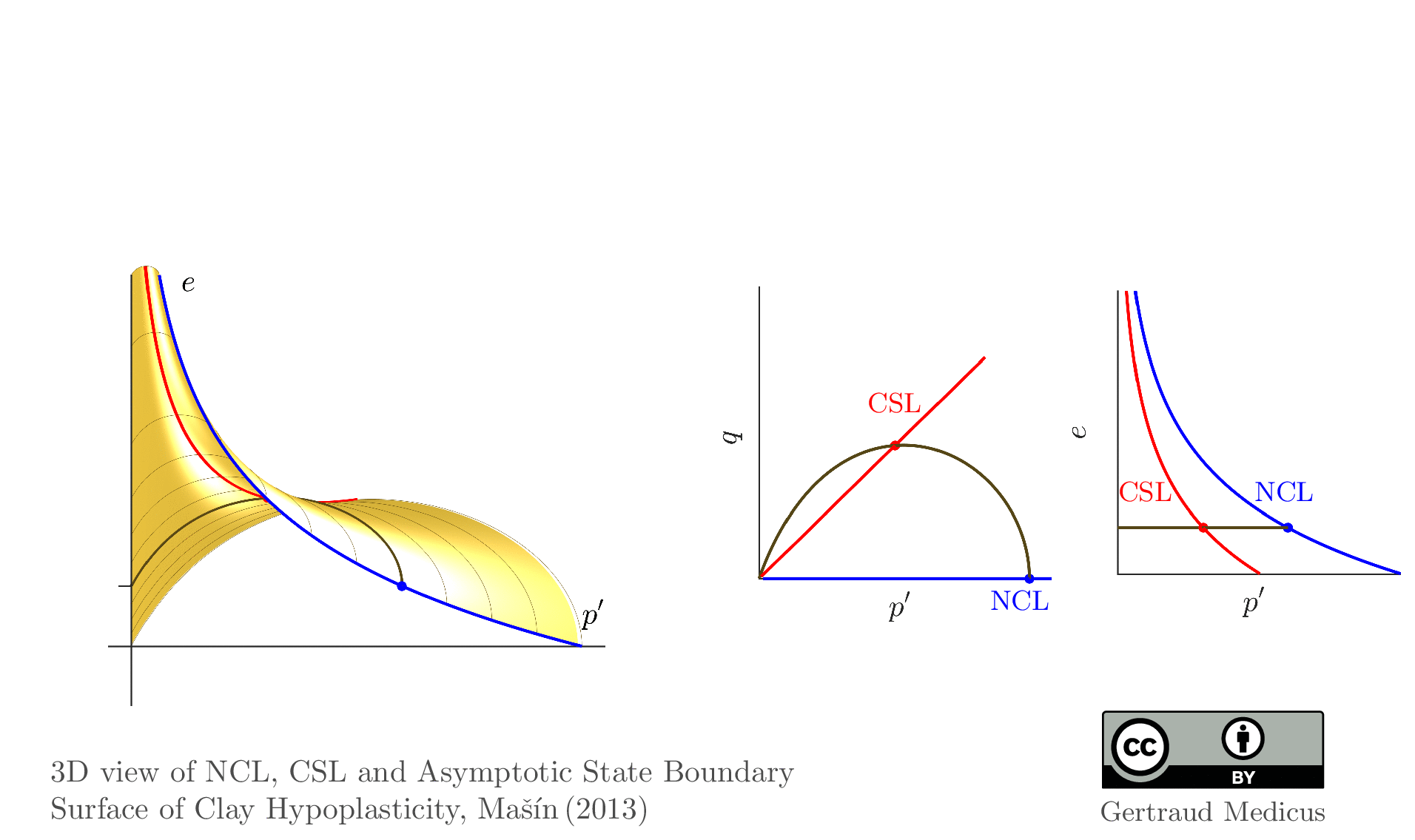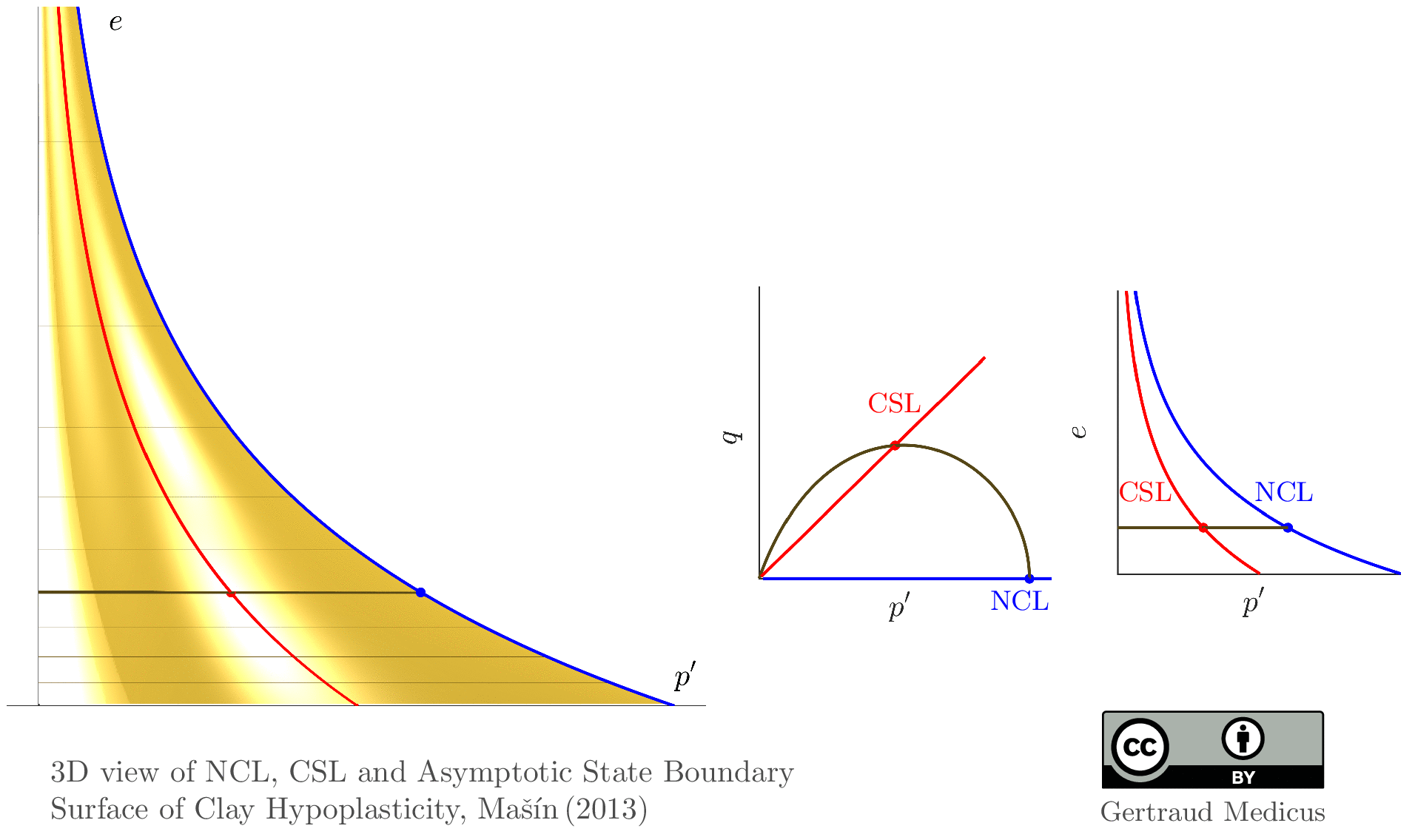
The Modified Cam Clay (MCC) model by Roscoe & Burland (1968) is an elasto-plastic hardening model, assuming associated flow. It includes concepts from Critical State Soil Mechanics as the Normal Compression Line (NCL) and the Critical State Line (CSL).
Click on the images to enlarge them. You can download the GIF files directly. Below each figure, you can also download corresponding PDF files.
State boundary surface of the Modified Cam Clay model
- Here is the PDF animation where you can use control buttons (pause/speed up/…). It can be viewed for example in Acrobat Reader (except on mobile devices).
- here is the PDF file which includes all slides.
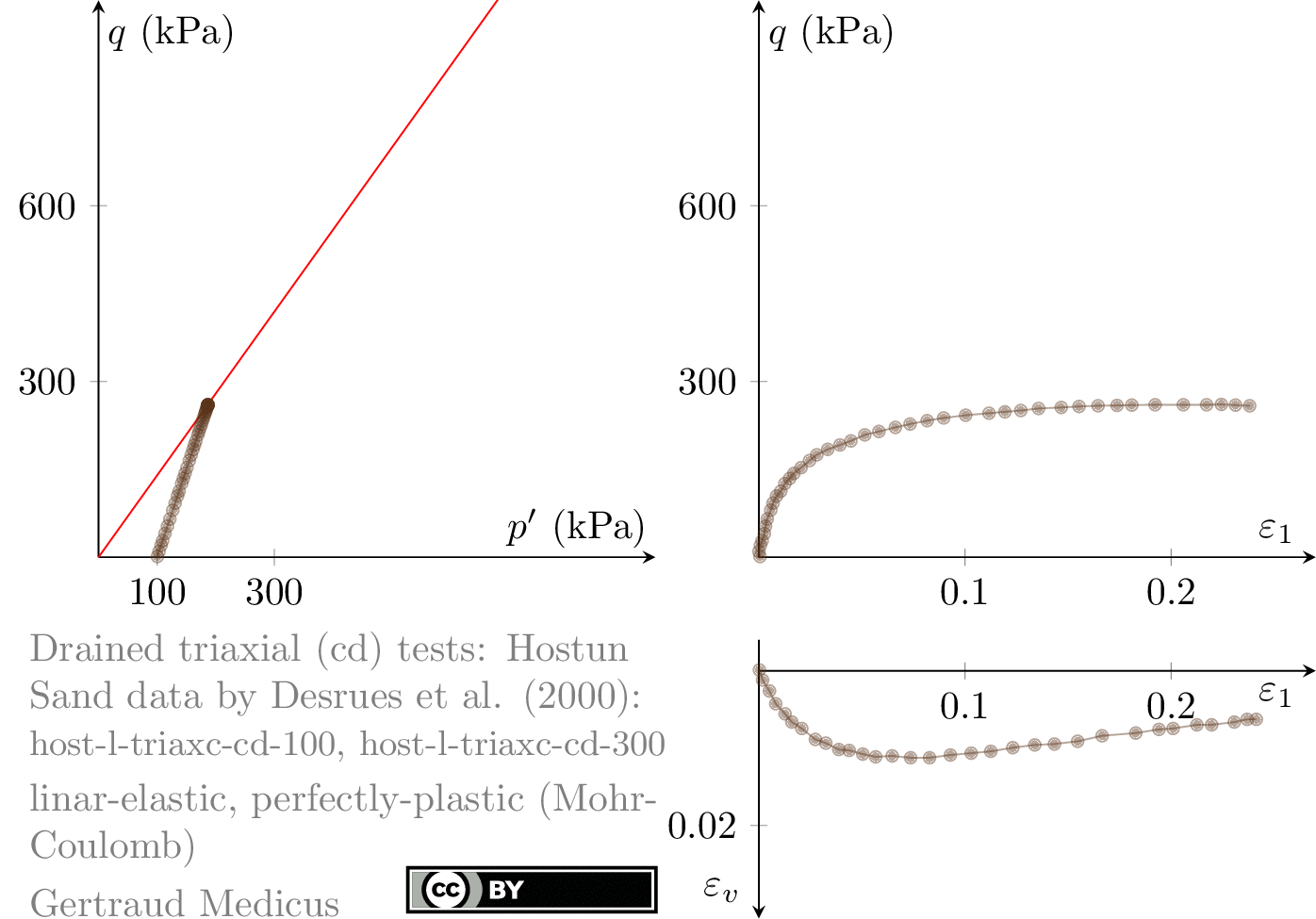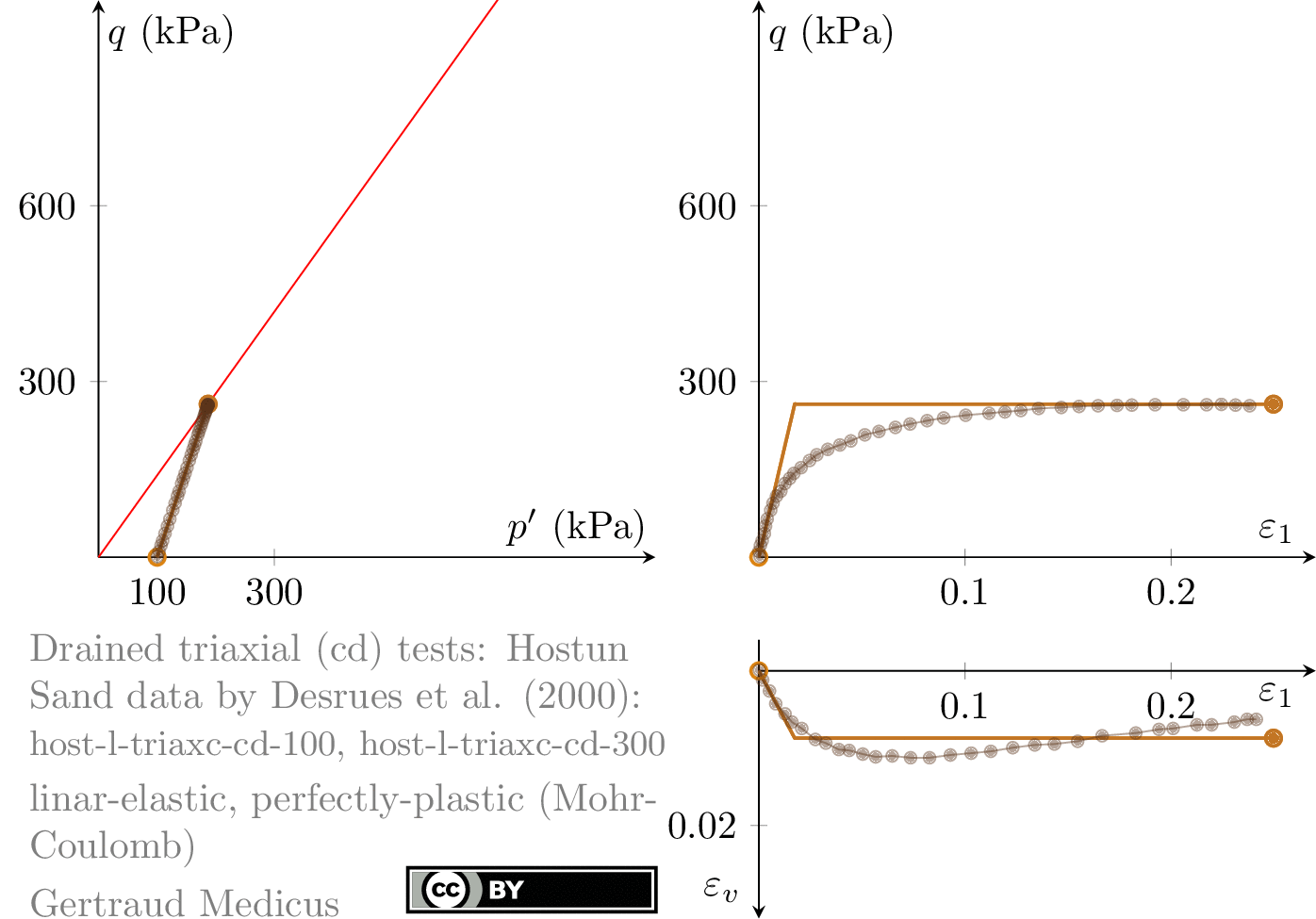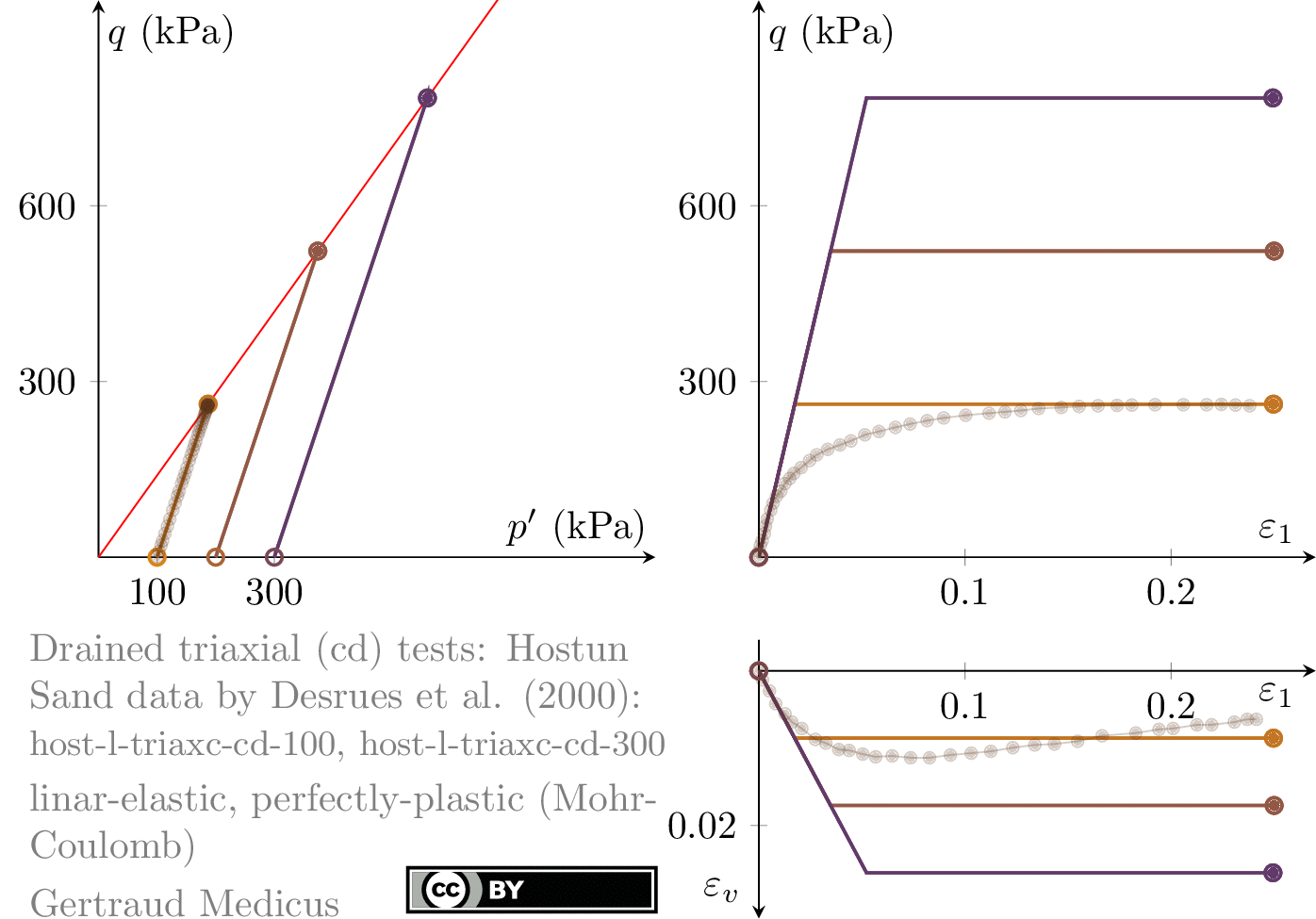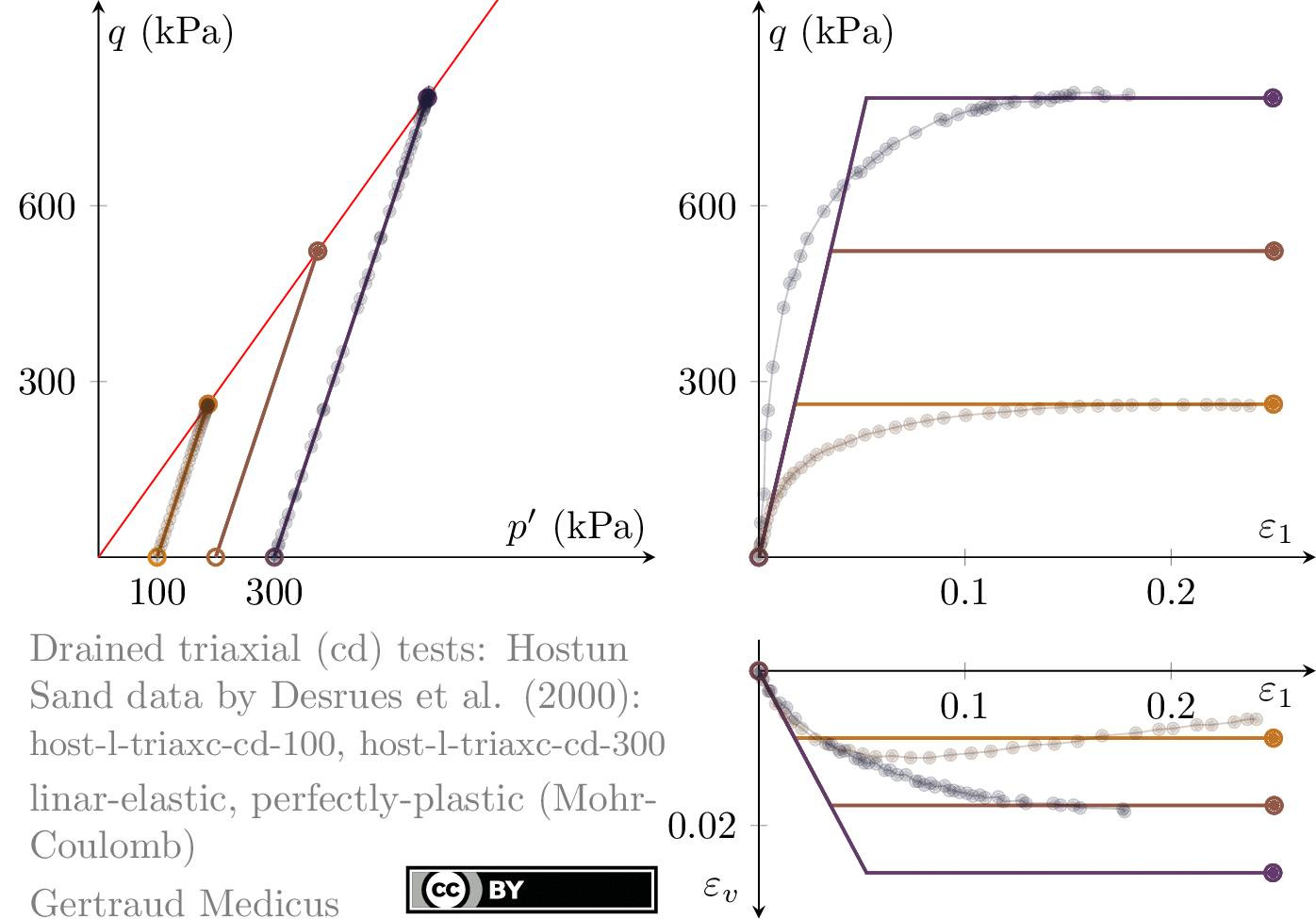
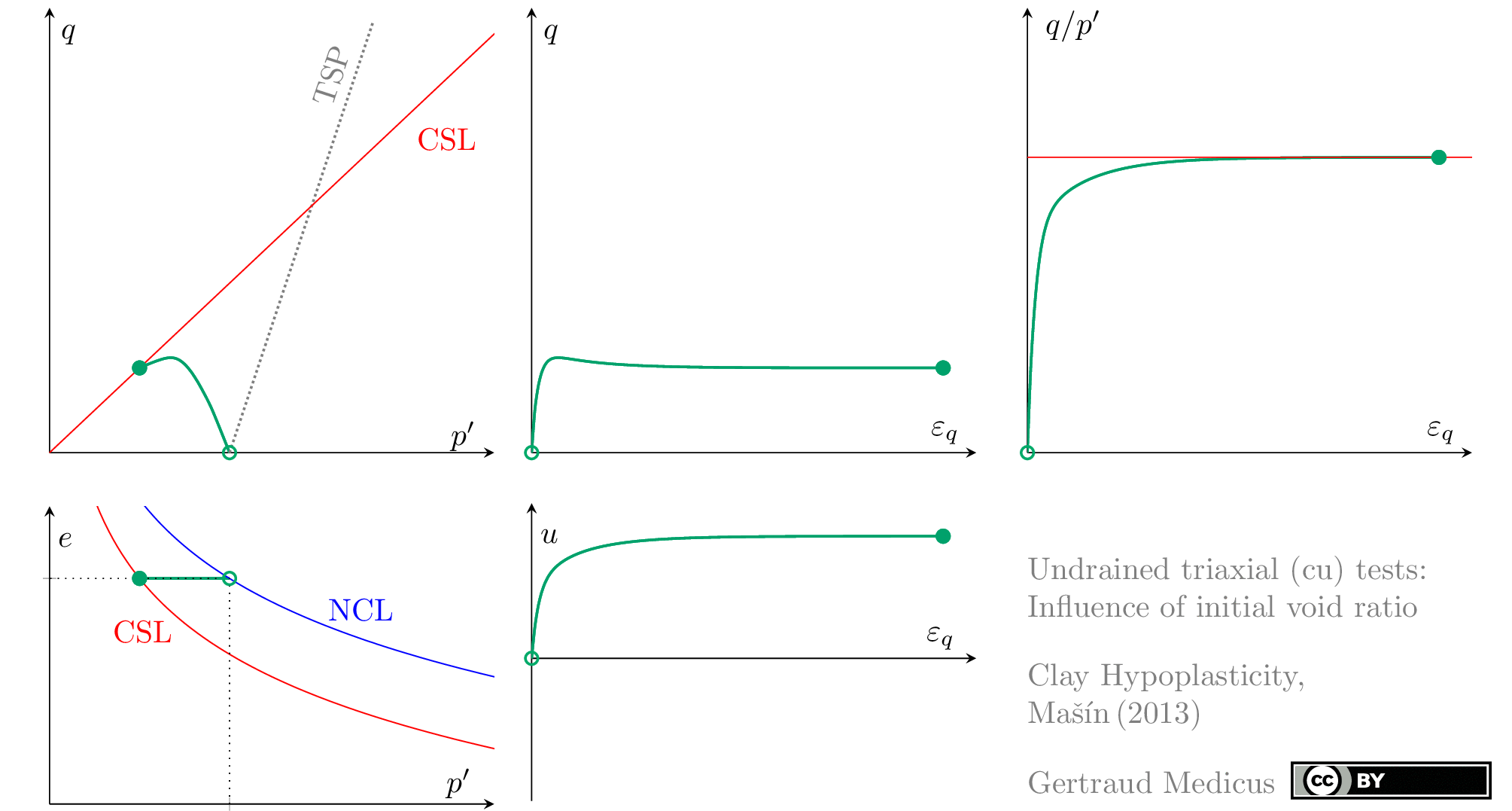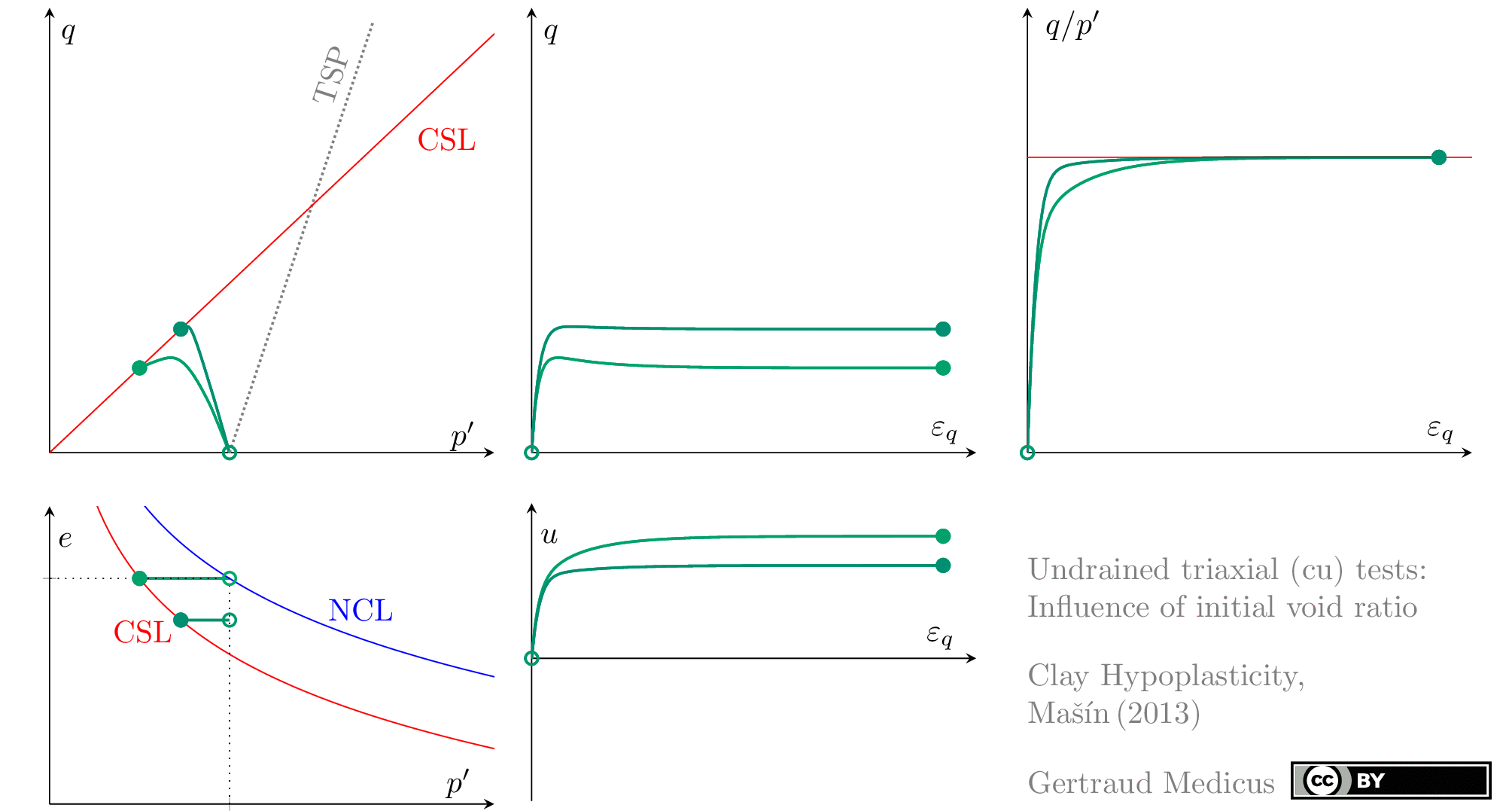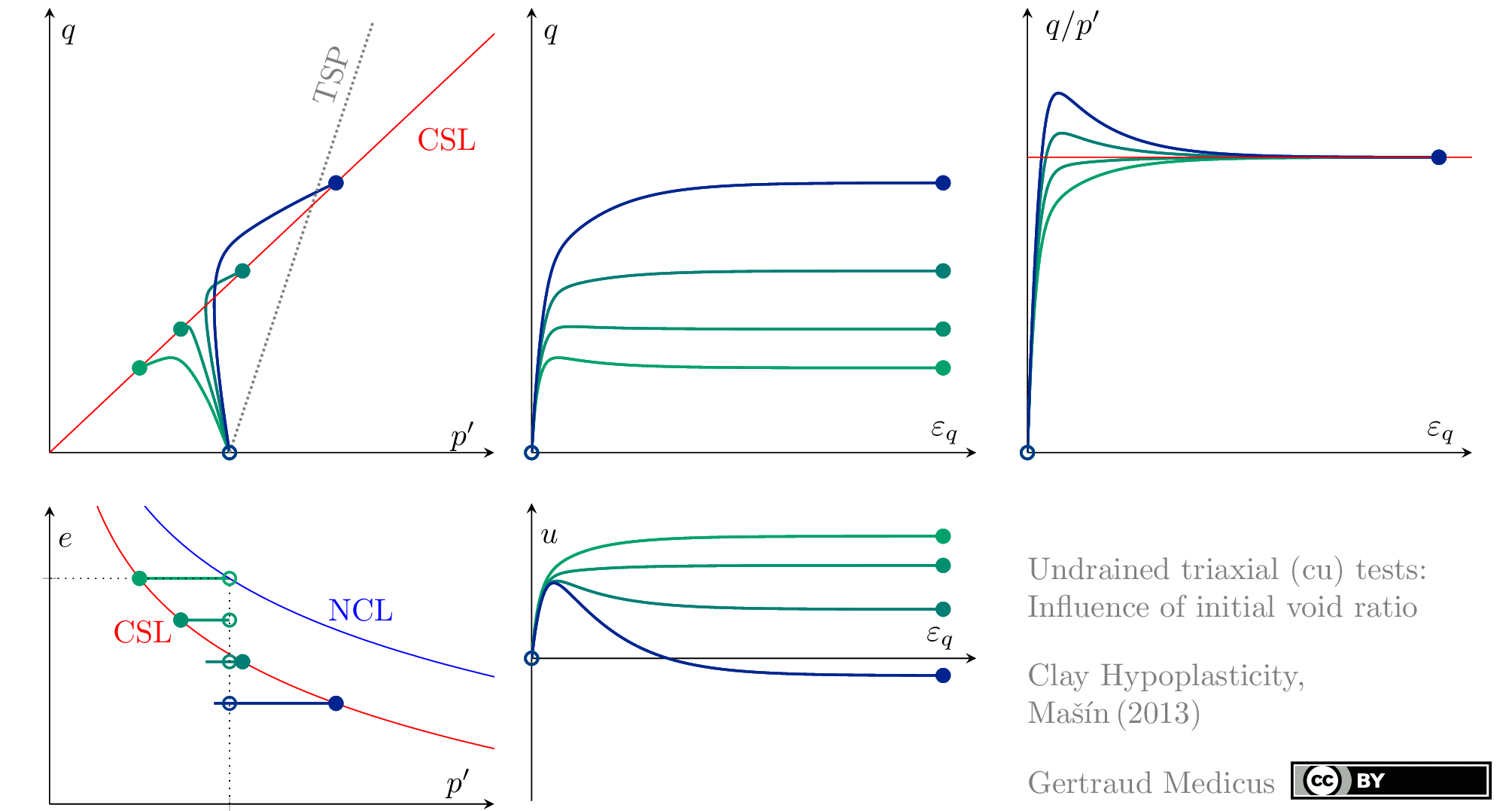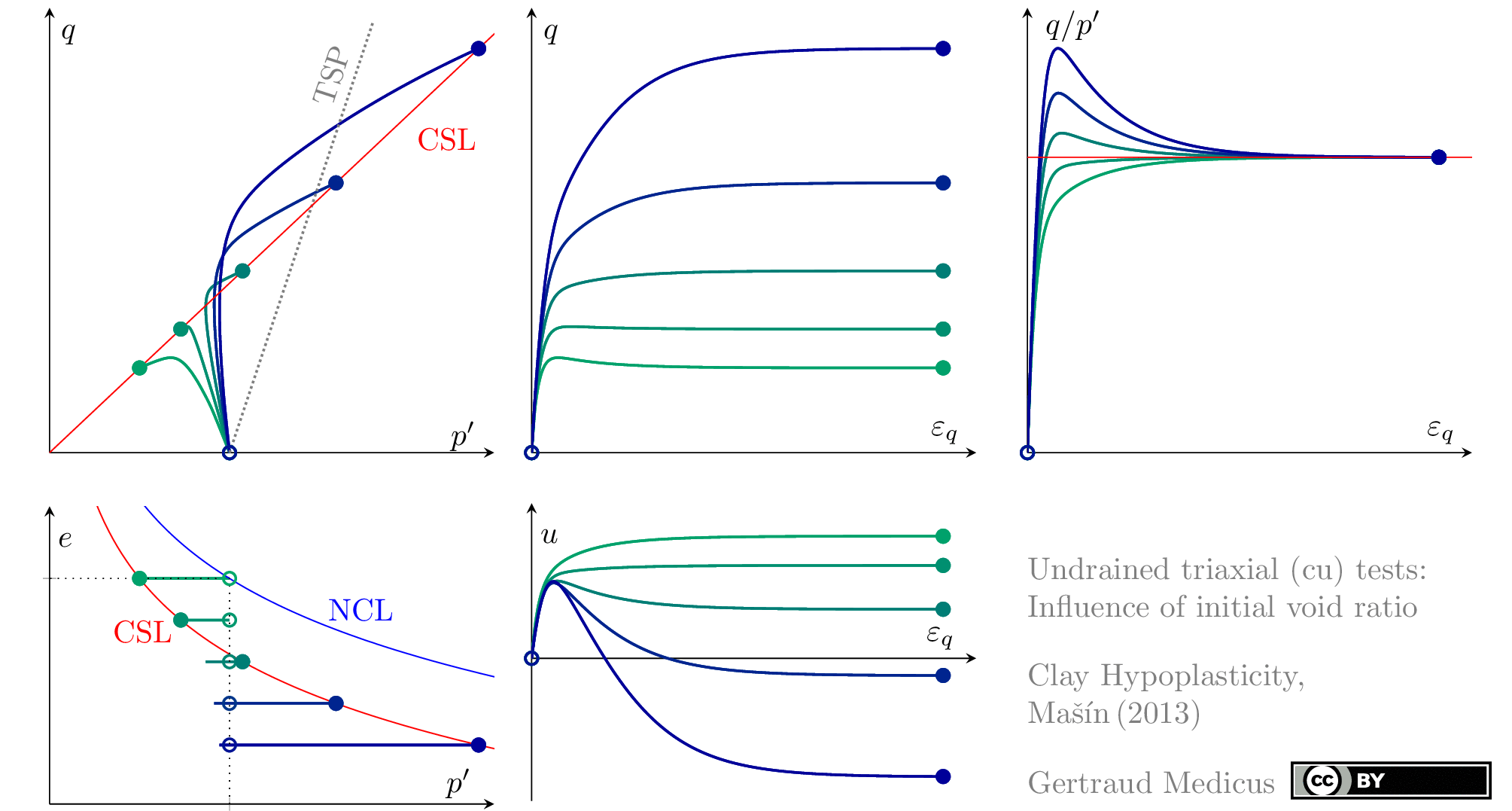
Drained (cd) triaxial tests
Undrained (cu) triaxial tests
normally consolidated:
‘TSP’ indicates the total stress path
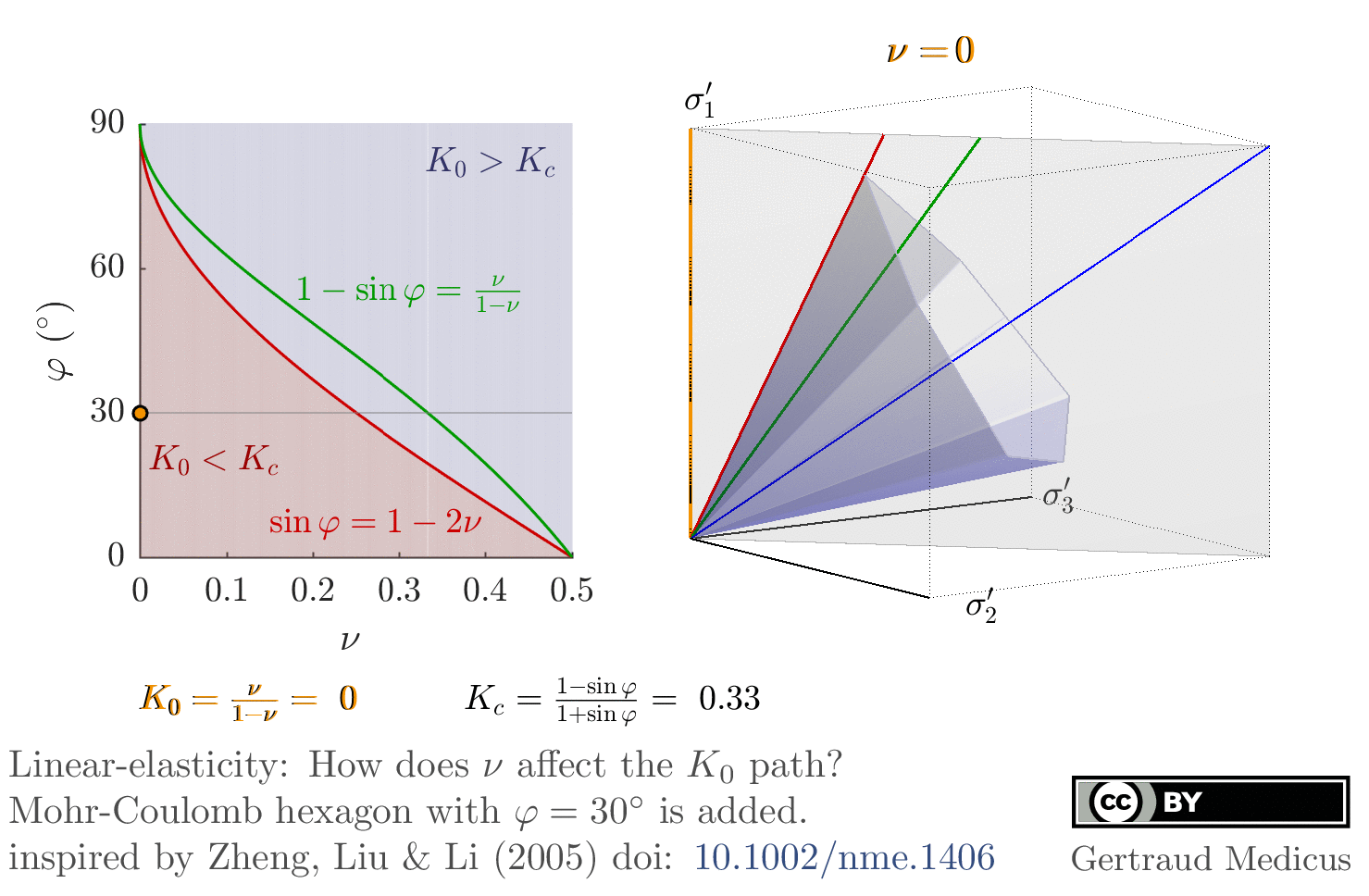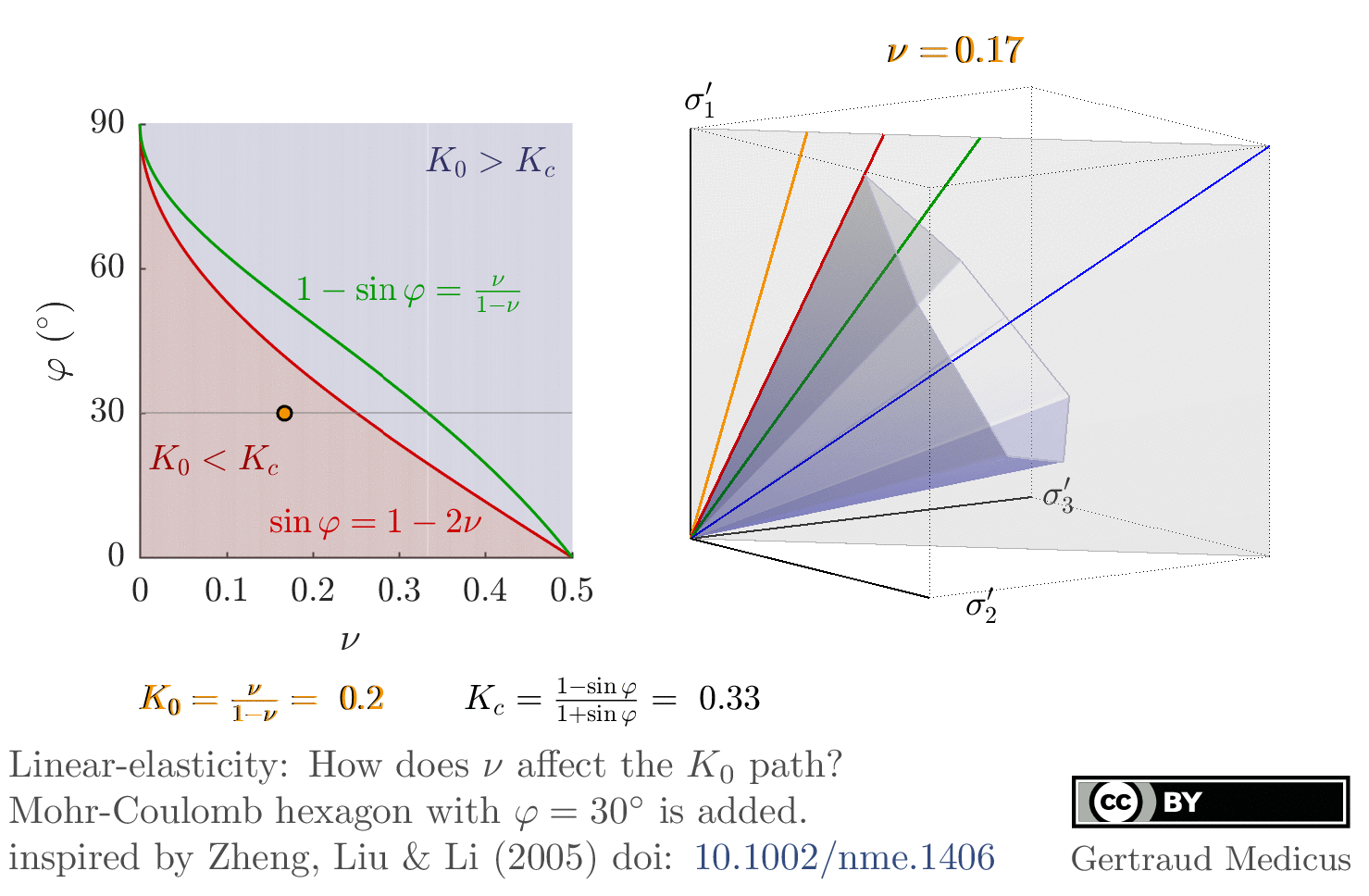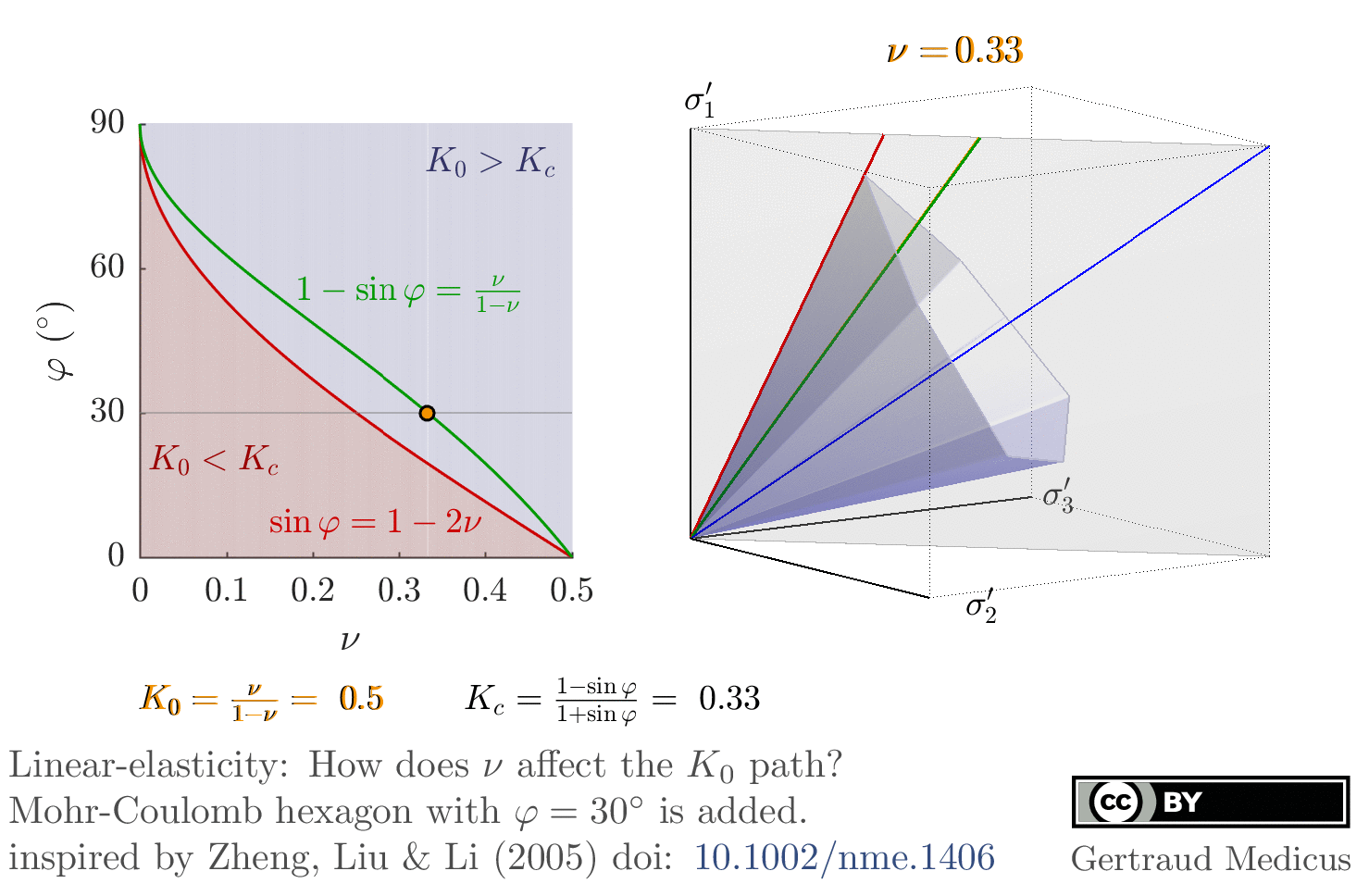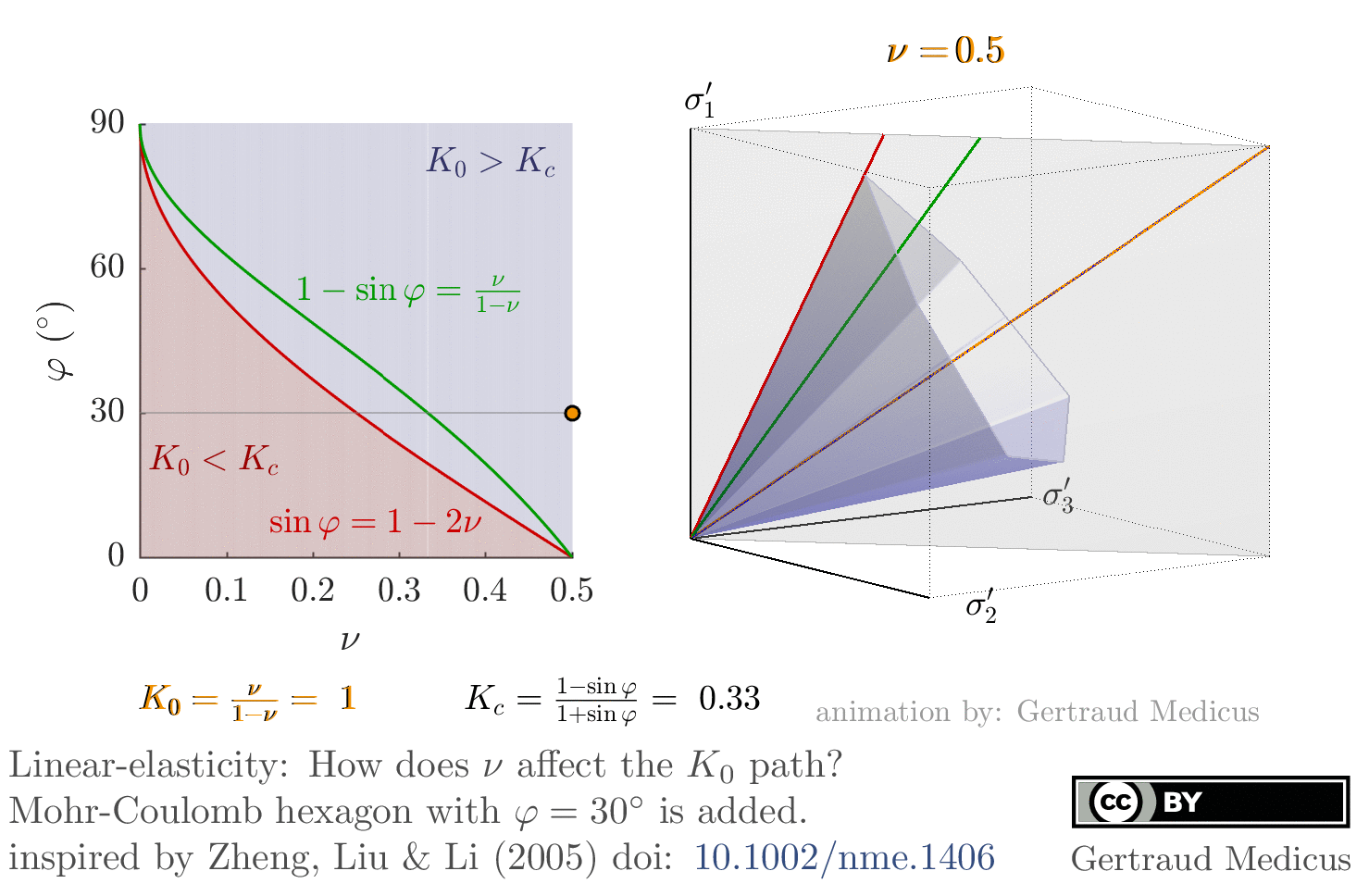
Linear-elasticity: How does ν affect the K₀-stress path (the stress path under oedometric compression). Mohr-Coulomb hexagon for φ = 30°, c = 0 is added; inspired by Zheng, Liu & Li (2005): doi: 10.1002/nme.1406 φ –ν inequality, sin φ ⩾1 – 2ν
- Here is the PDF animation where you can use control buttons (pause/speed up/…). It can be viewed for example in Acrobat Reader (except on mobile devices).
- here is the PDF file which includes all slides.
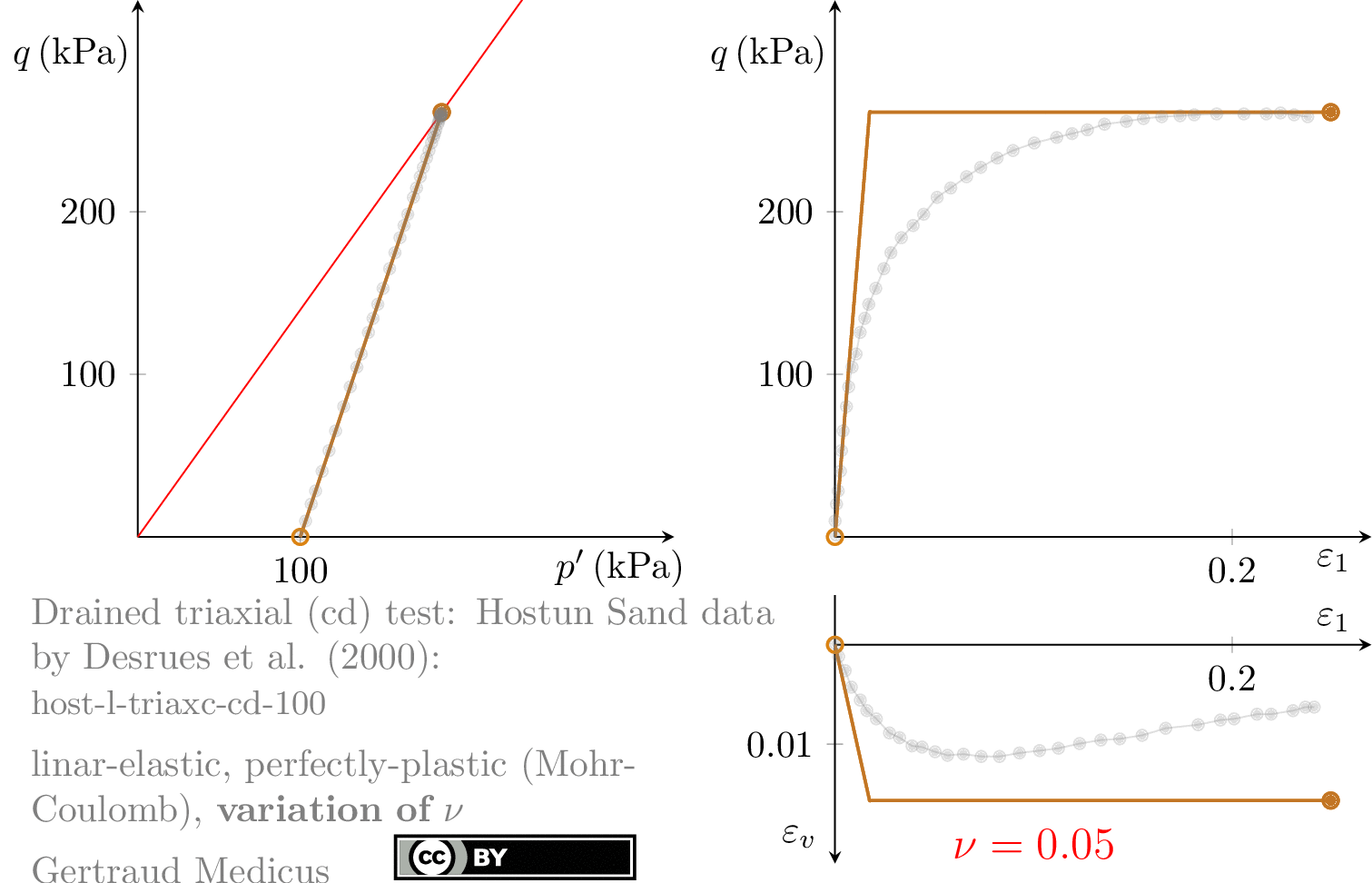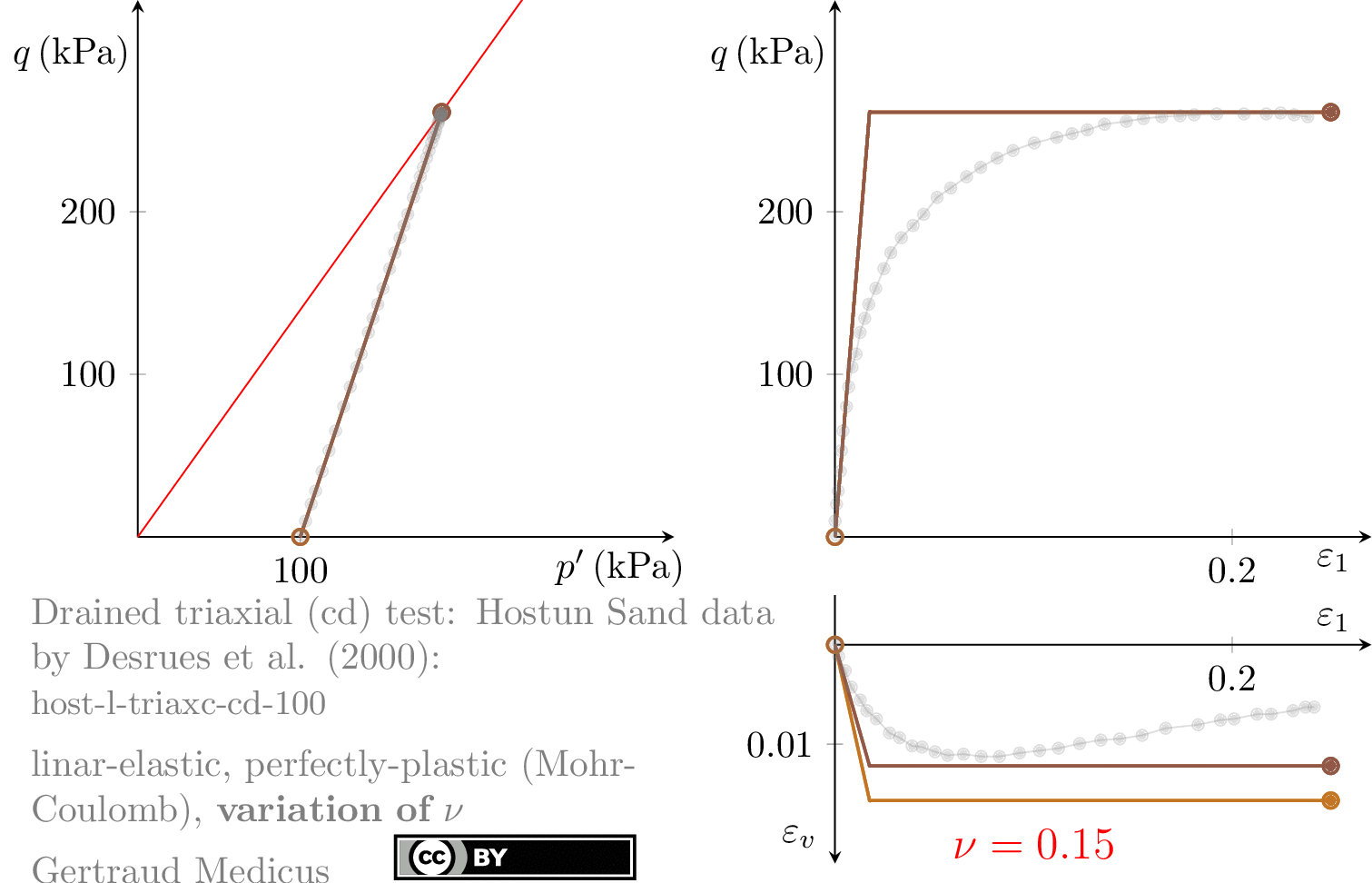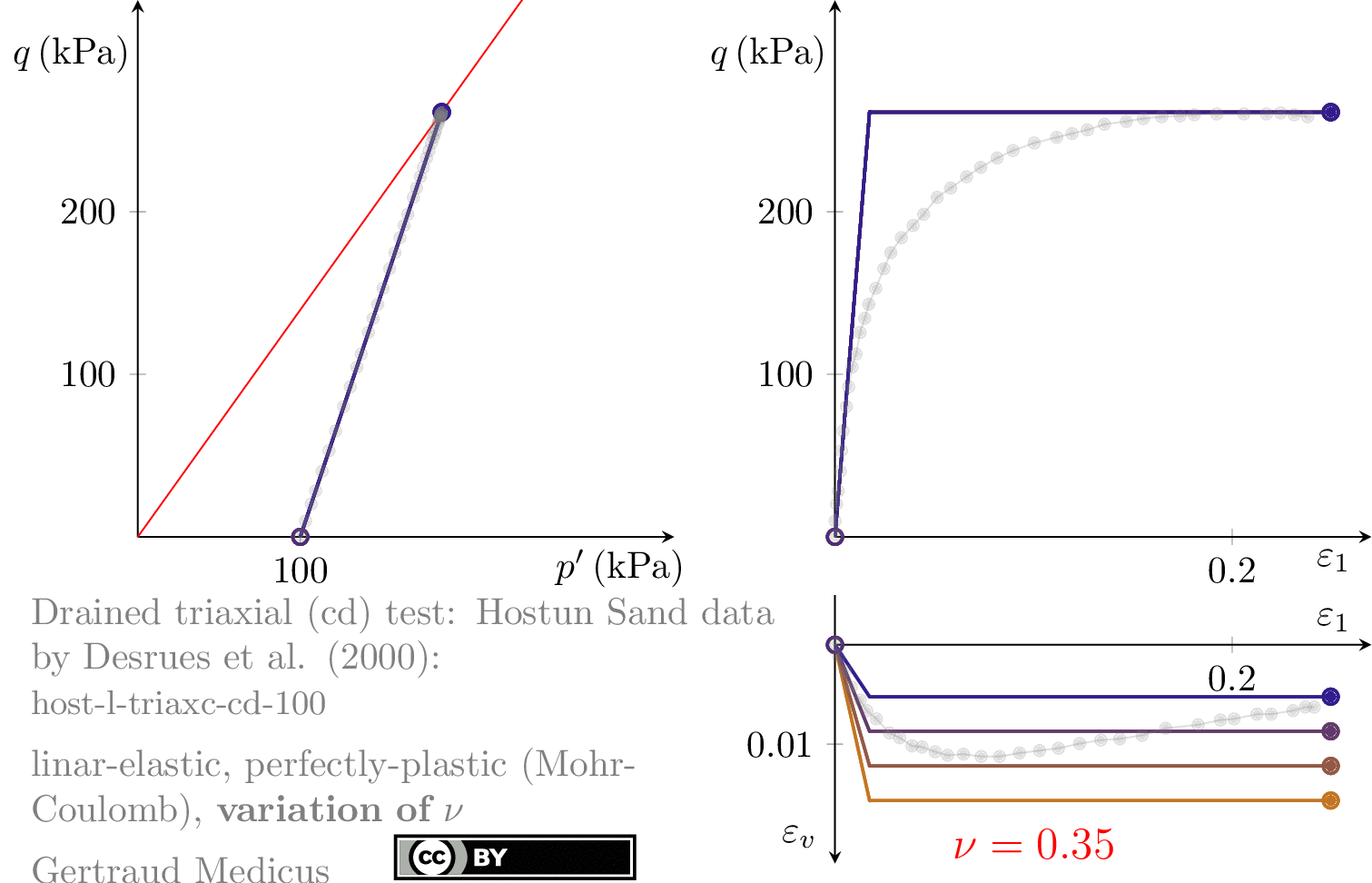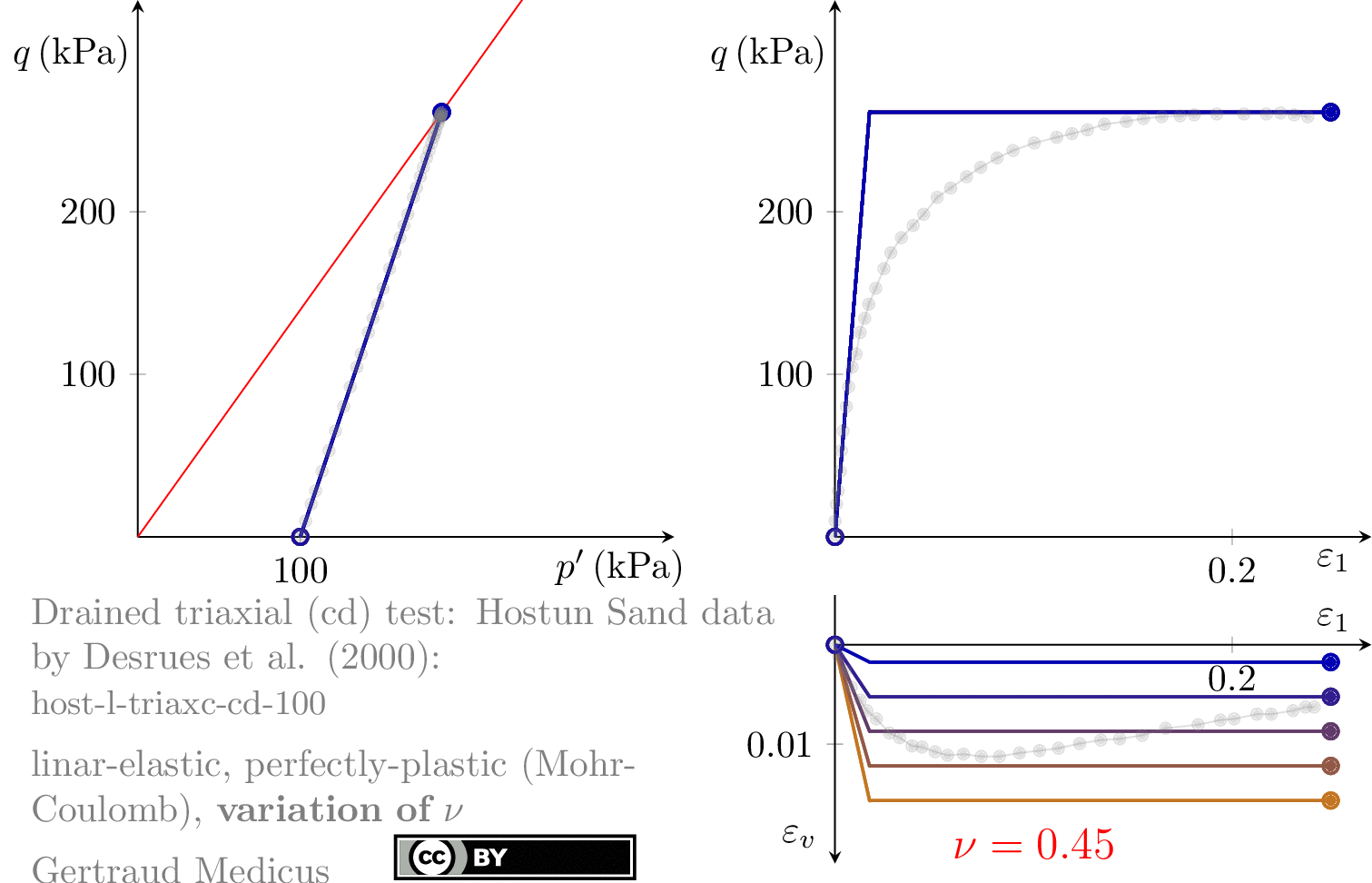
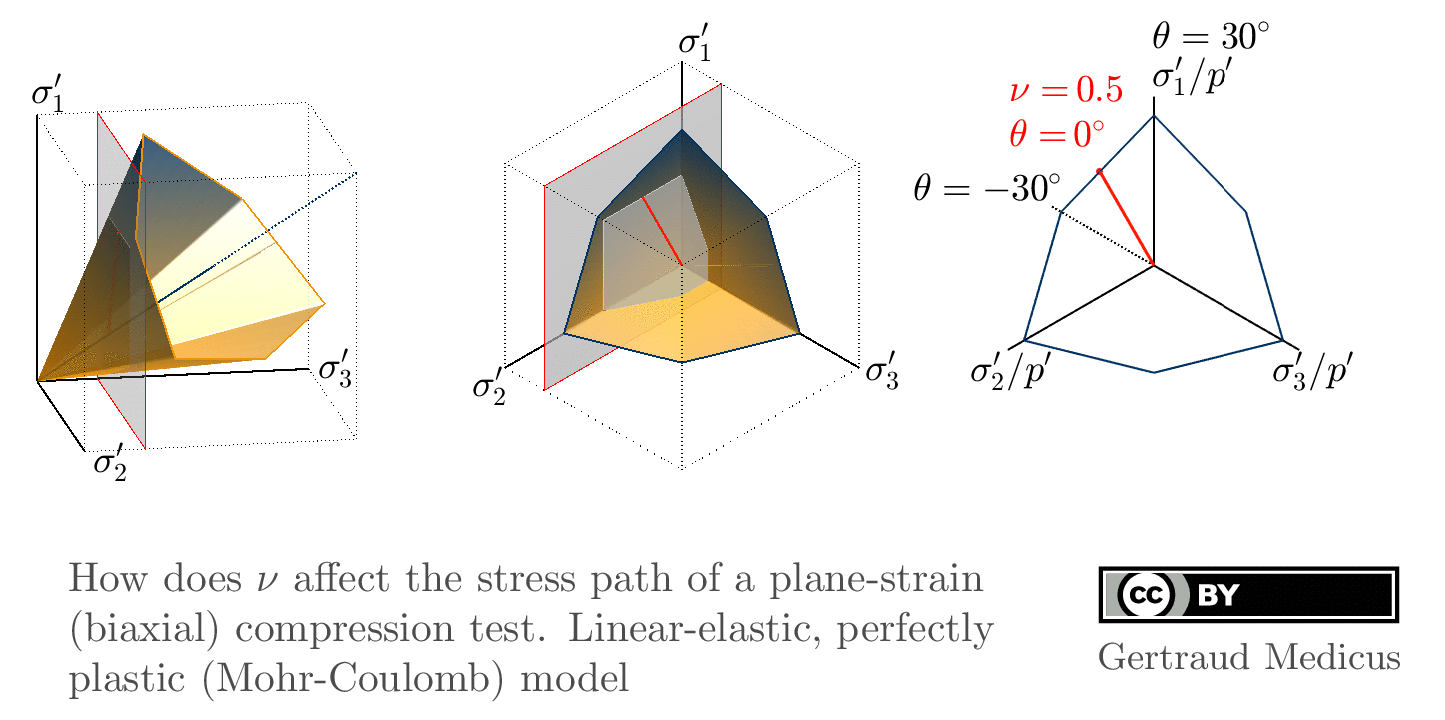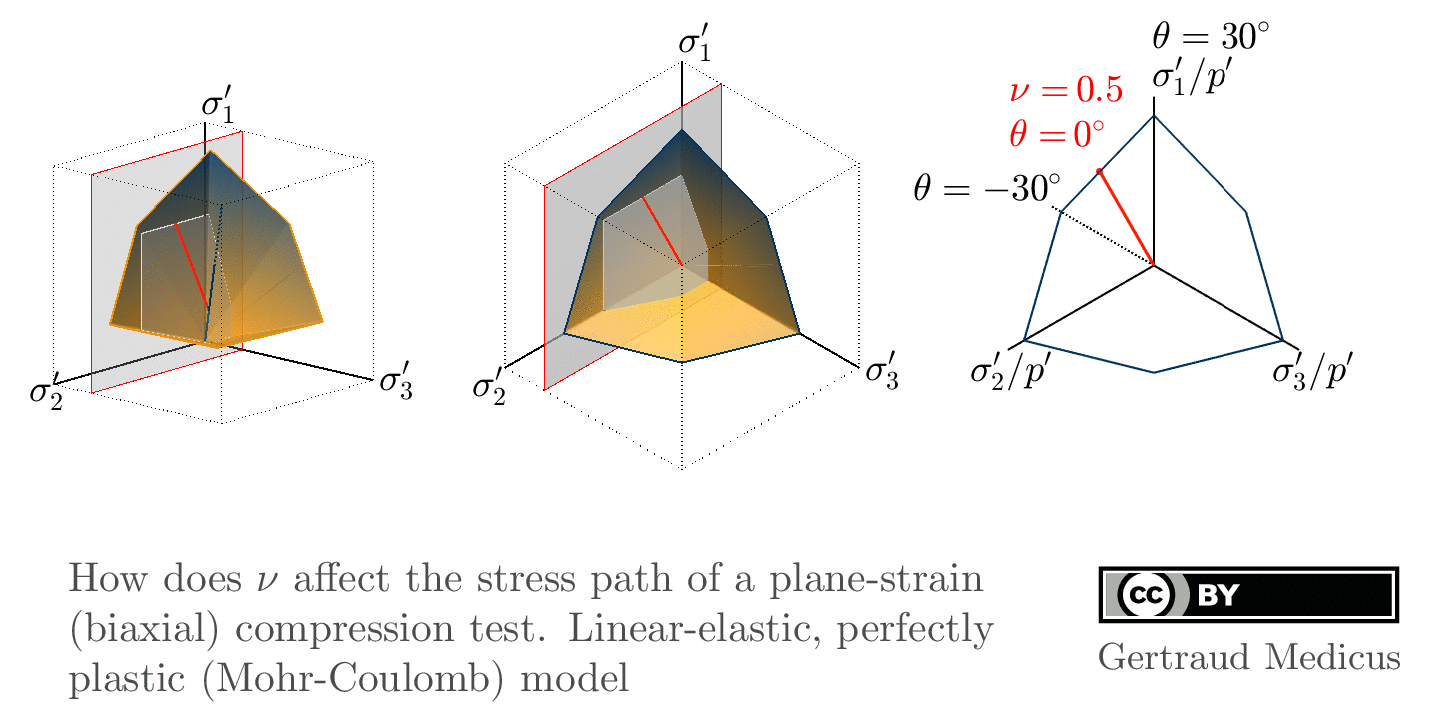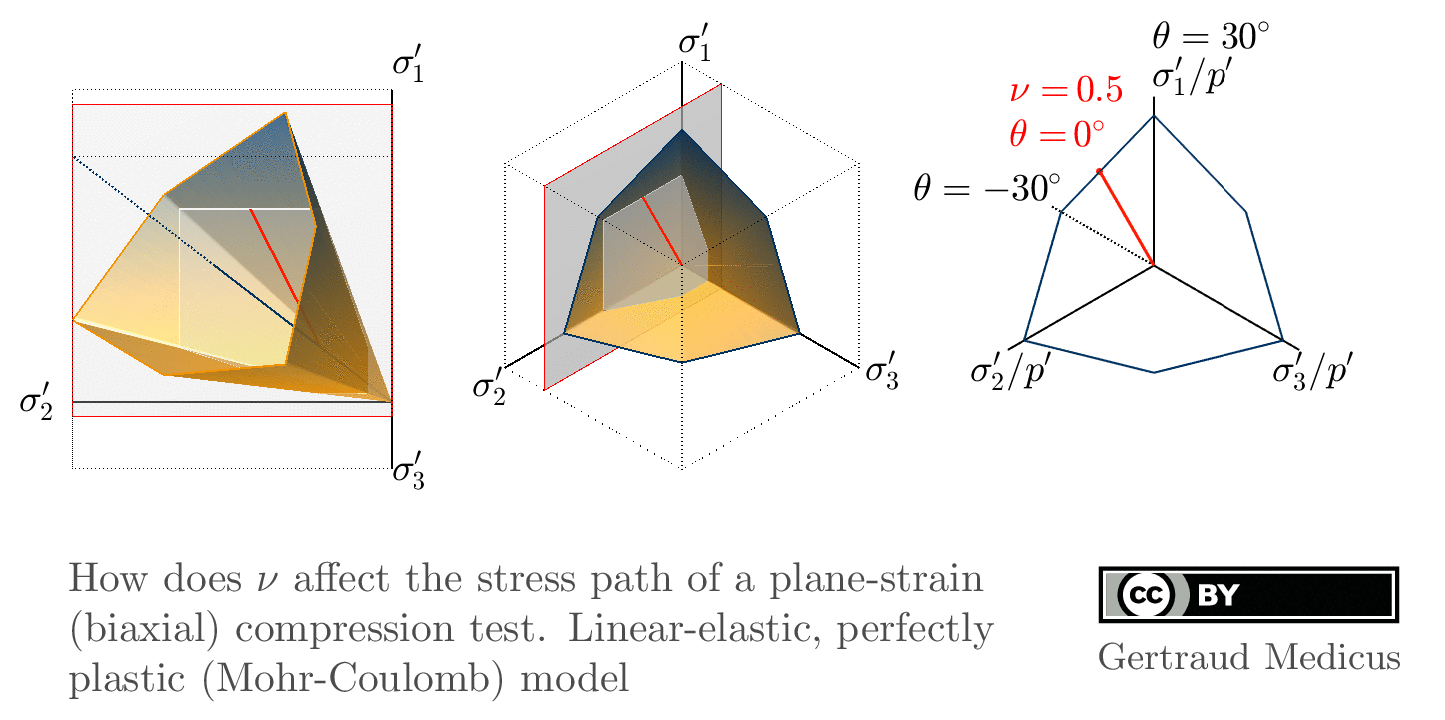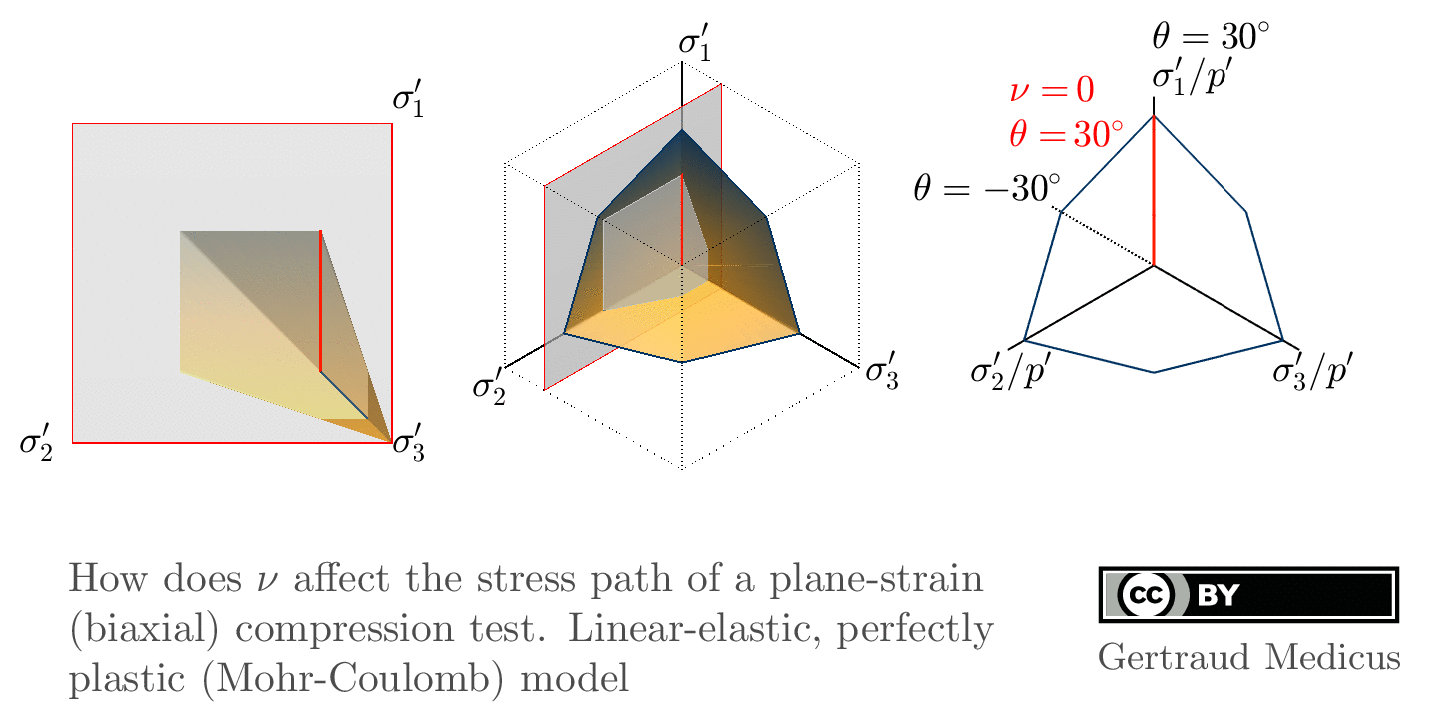
How does ν affect the stress path of a plane-strain (biaxial) compression test. Linear-elastic, perfectly plastic (Mohr-Coulomb: φ = 30°, c = 0, ψ = 0°) model.
The interactive graphics below have been created with GeoGebra
Sign convention: Tensile stresses (+), compressive stresses (-)
+i/-i: isotropic compression/extension, o: oedometric compression, +c/-c: undrained triaxial compression/extension
The figure below shows the response envelope of an elastic model (Hook’s law). You can move the point P (blue bullet) in the Rendulic plane of strain rate space (left) and vary shear modulus and bulk modulus.
click to enlarge
The figure below shows the response envelope of sand hypoplasticity (von Wolffersdorff, 1996), which follows from an elastic response envelope L : ε̇, that is shifted by N ||ε̇||. You can move the point P (red bullet) in the Rendulic plane of strain rate space (left).
Thanks to Ivo Herle for providing the axisymmetric formulation of hypoplasticity in his PhD thesis (Herle, 1997). This has simplified the implementation with GeoGebra here 🙂
click to enlarge
The figure below shows the response envelope of sand hypoplasticity (von Wolffersdorff, 1996). You can move the point P (red bullet) in the Rendulic plane of strain rate space (left), vary state variables and parameters. You can also move the current stress state in the Rendulic plane of stress space (right). Click on the link below for a better view:


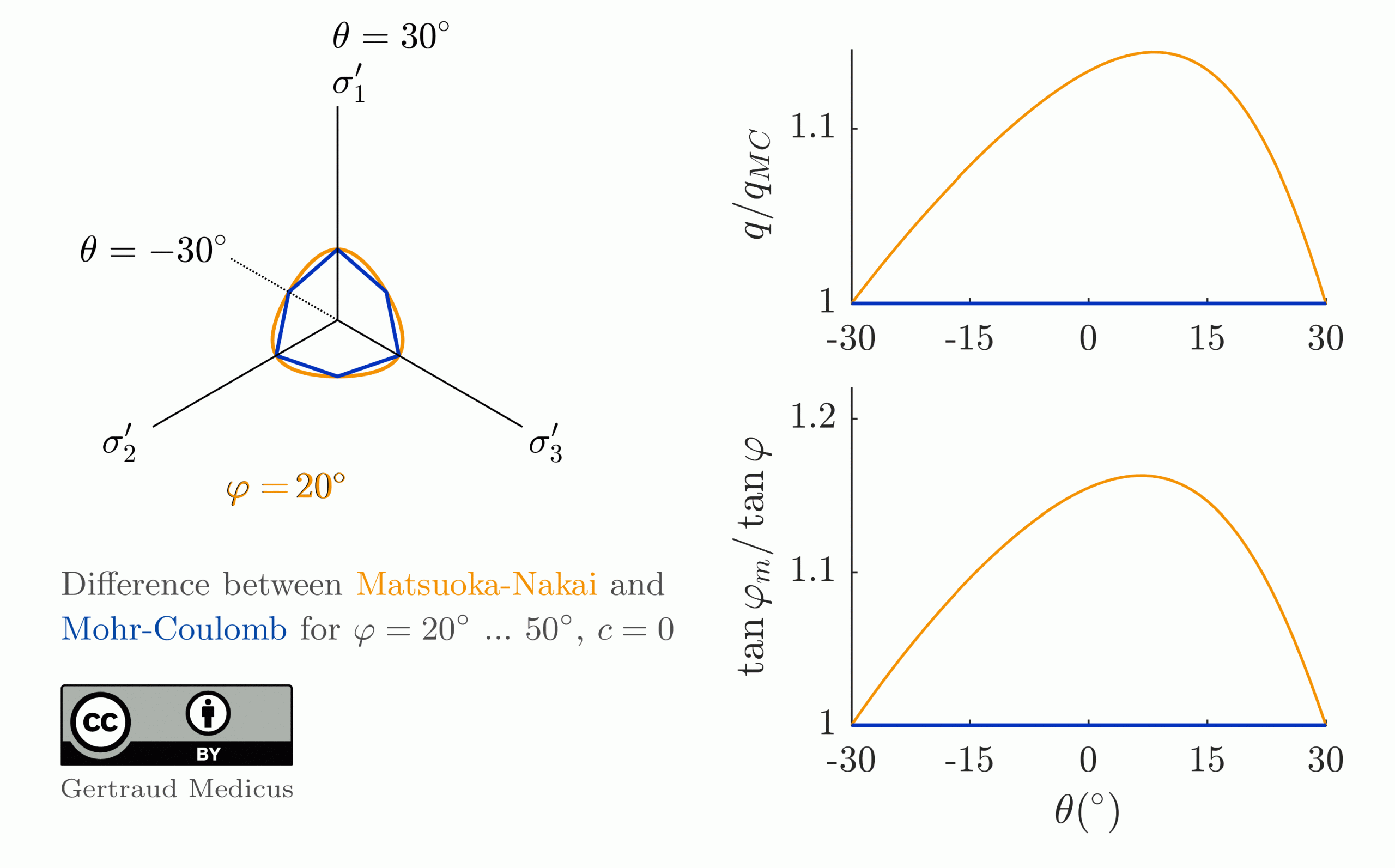
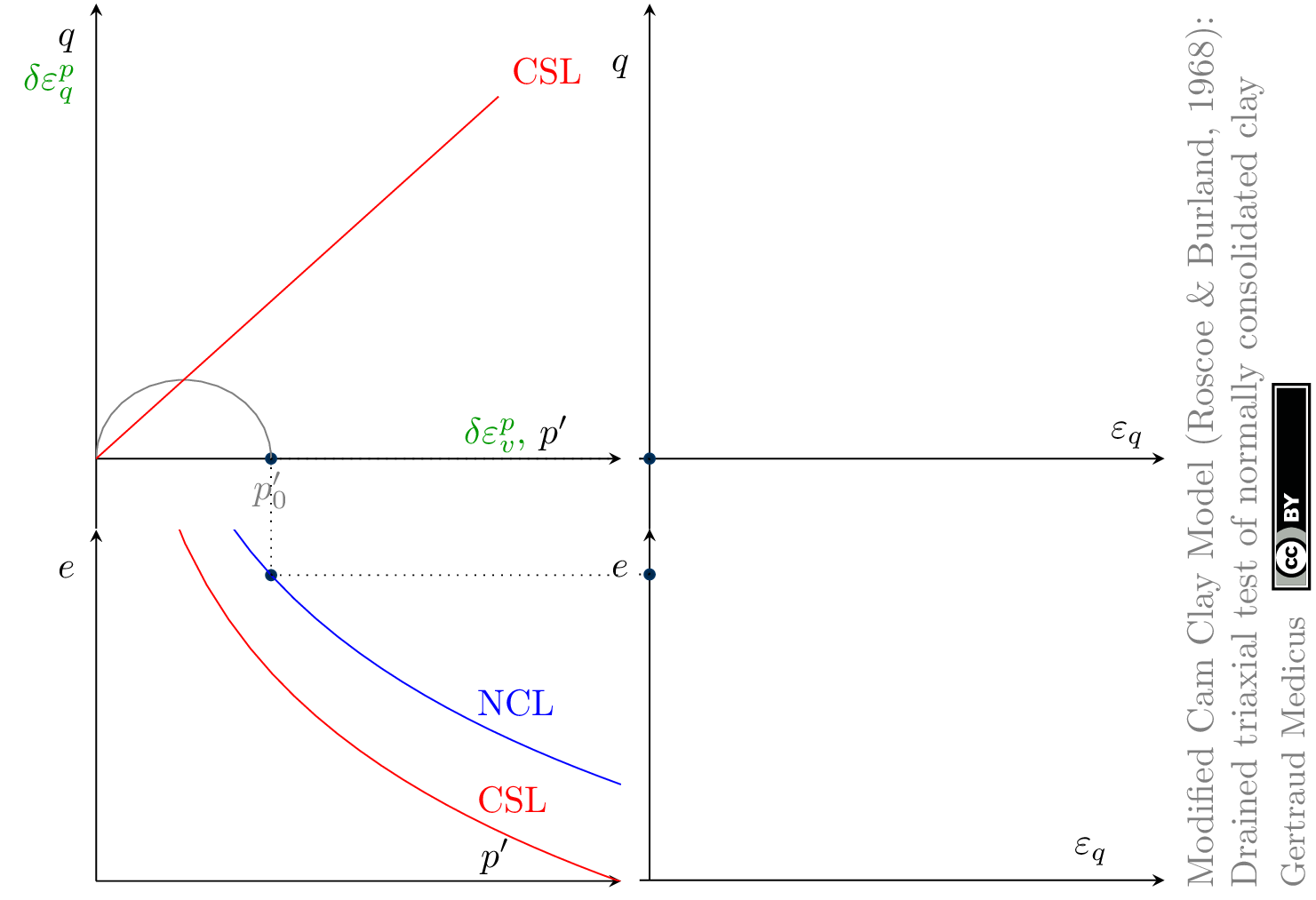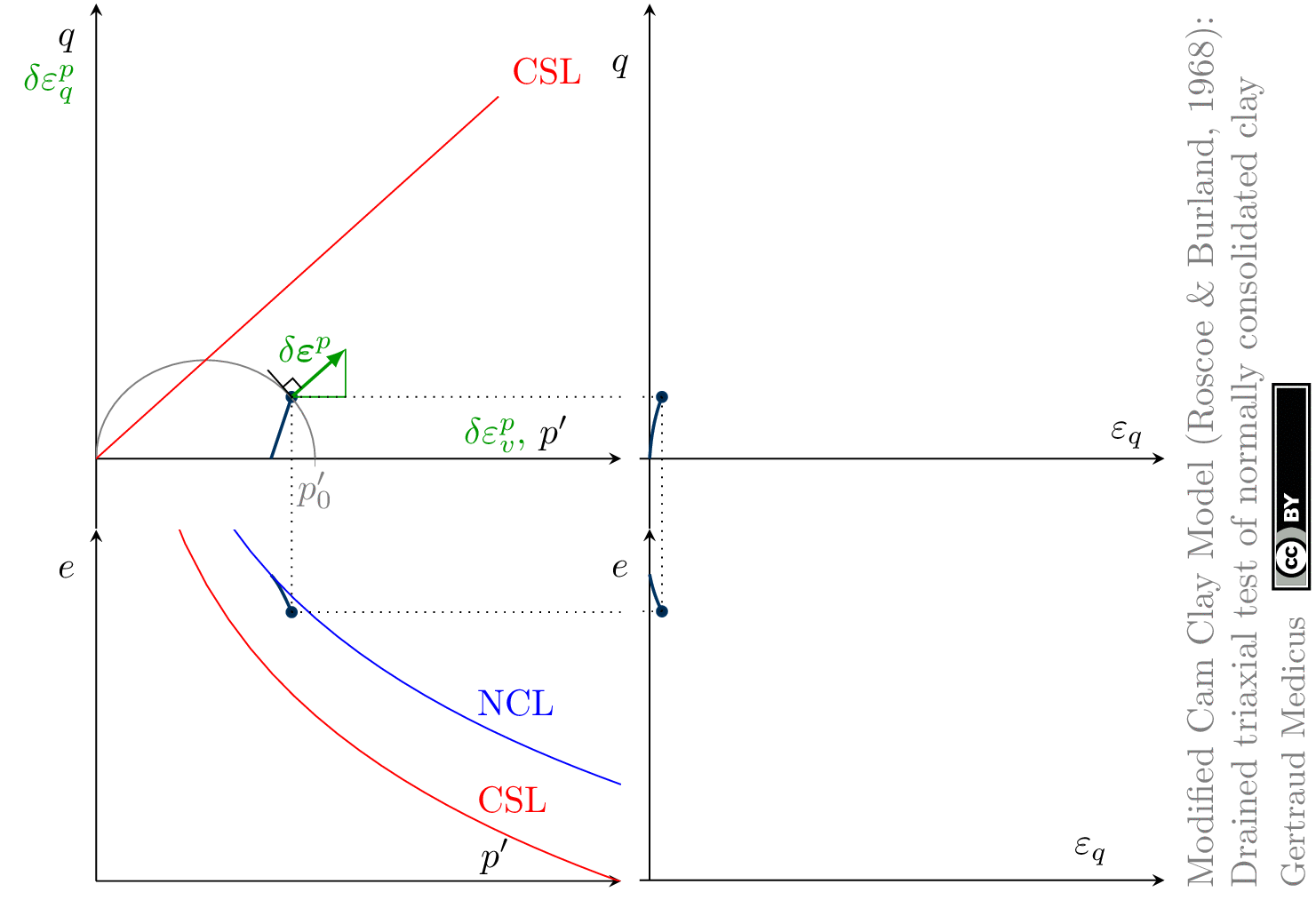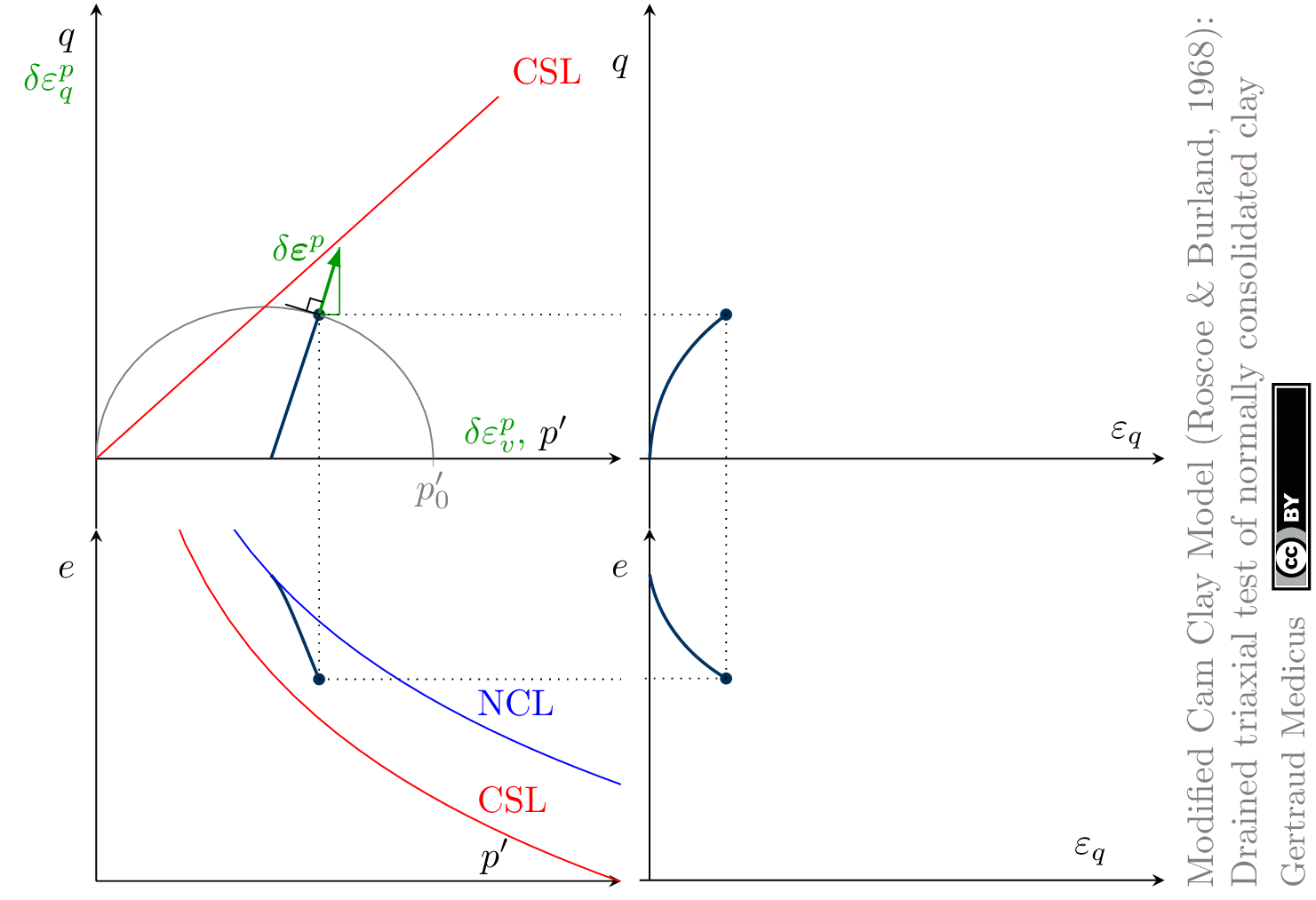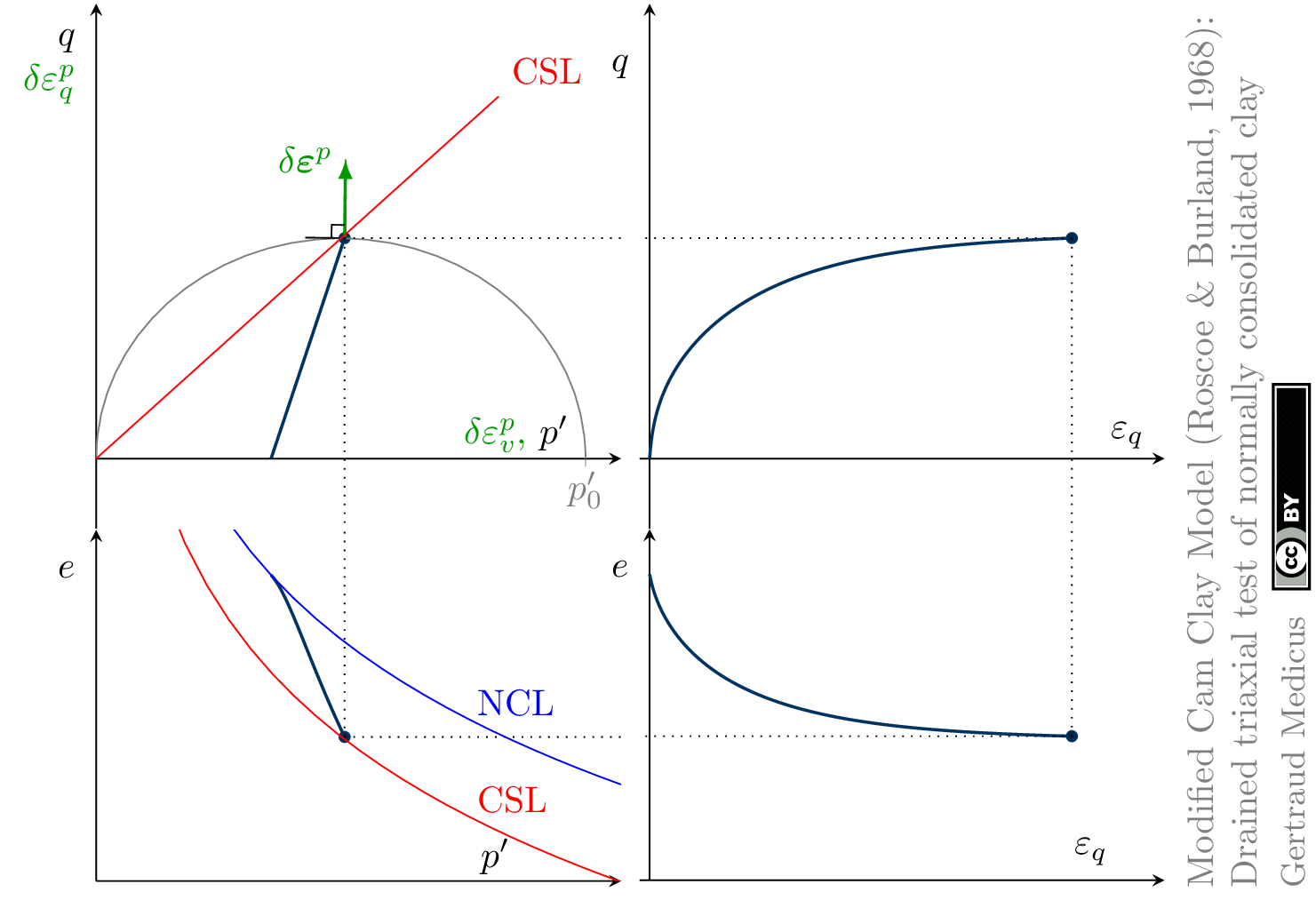
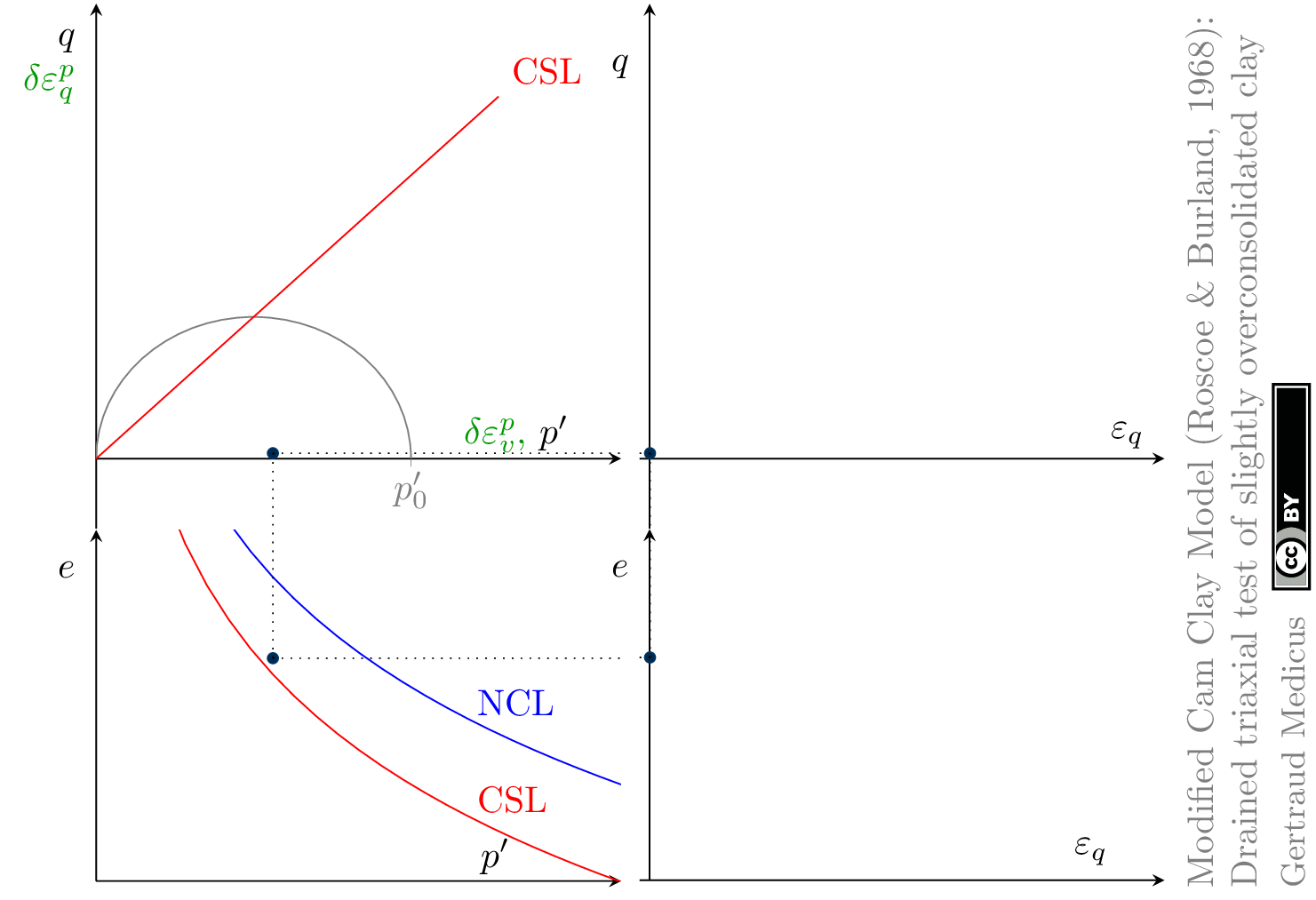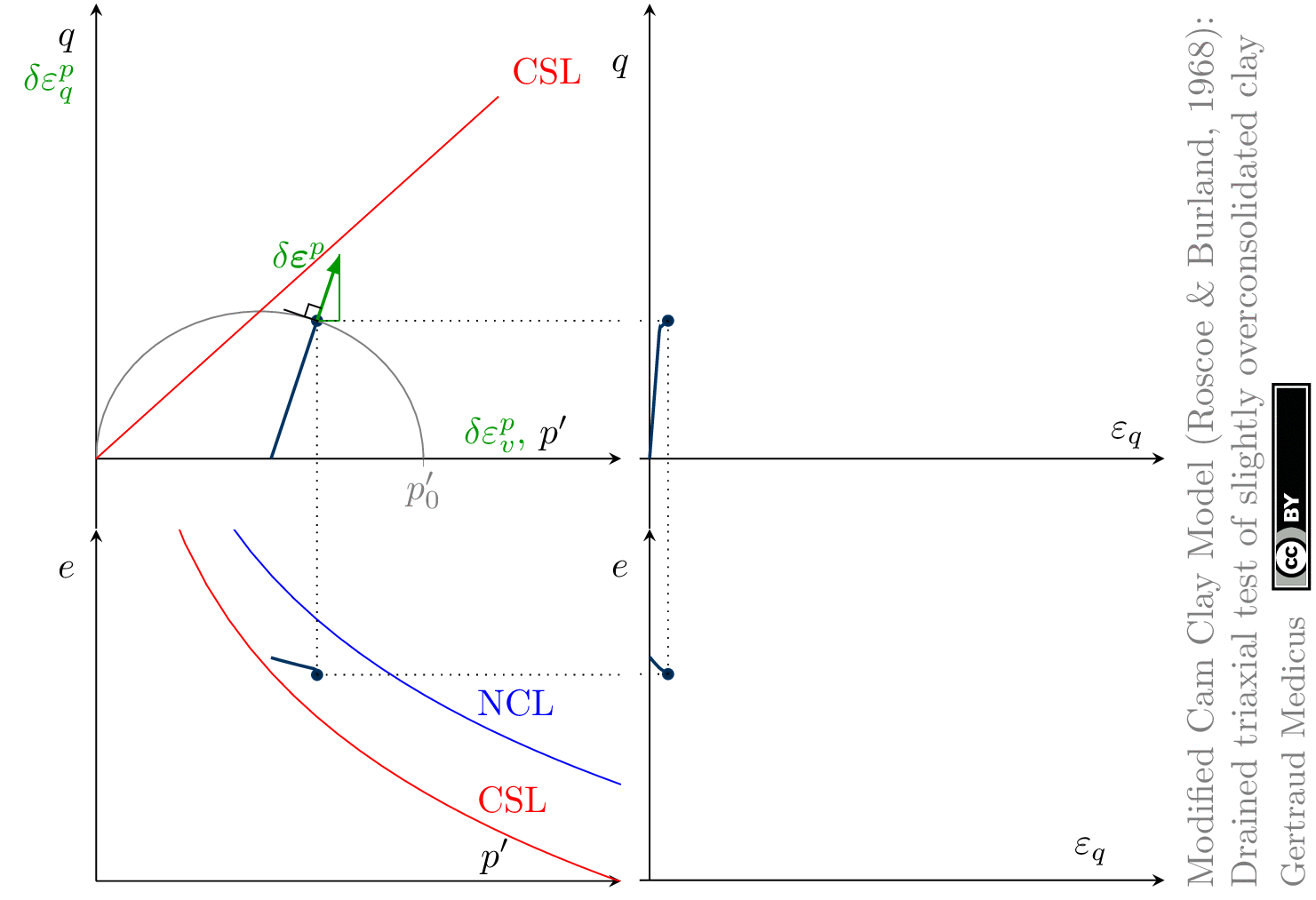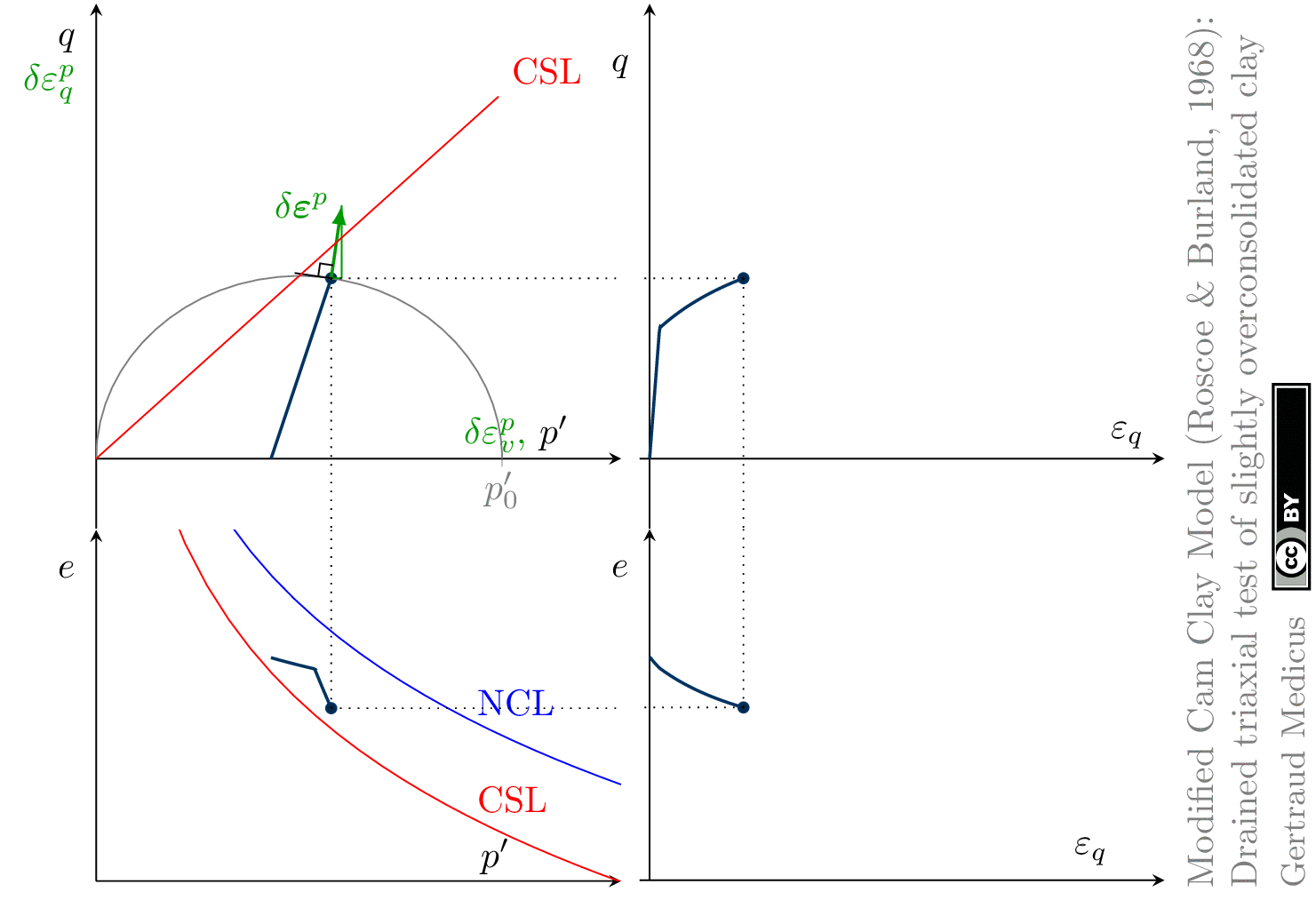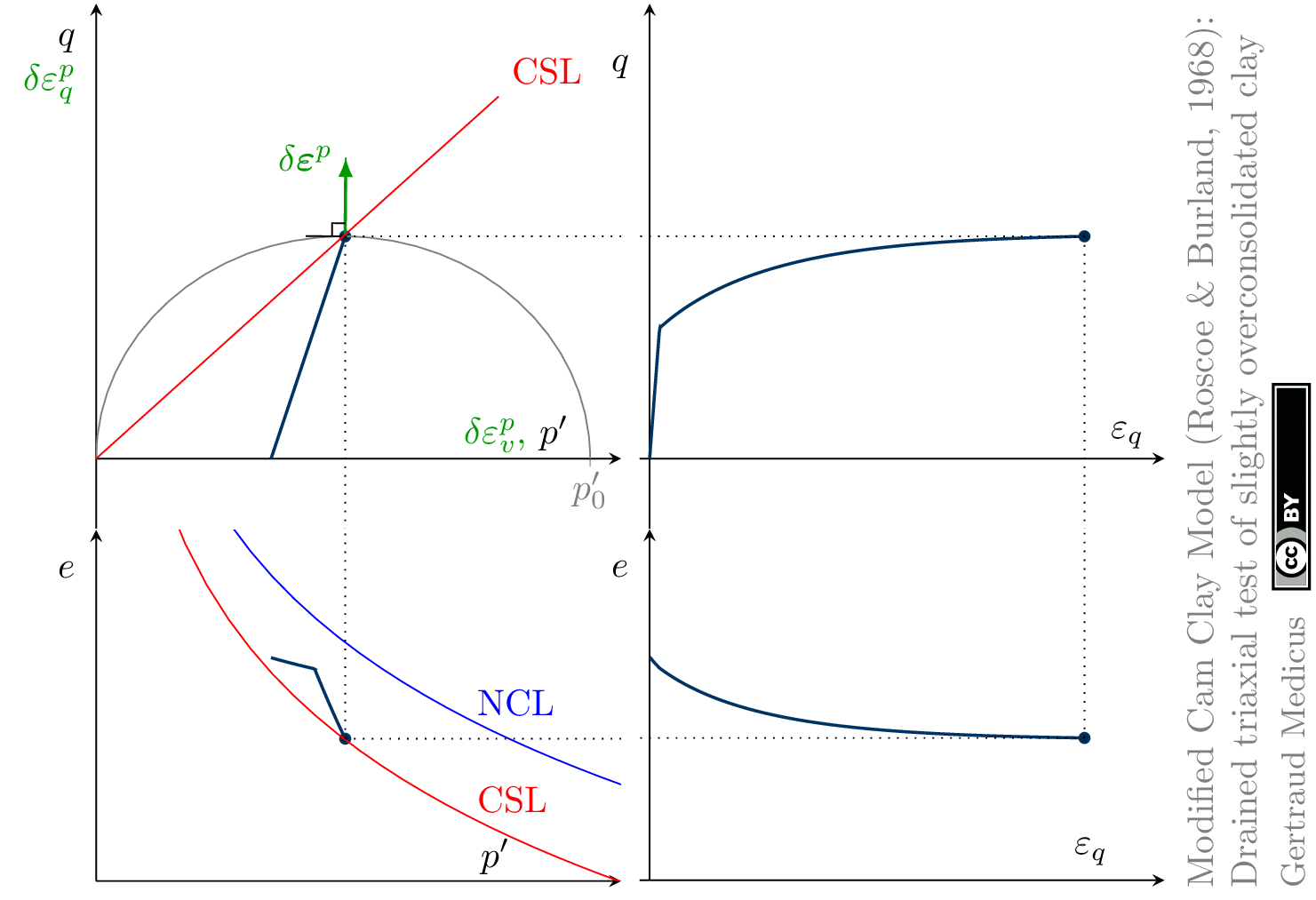
Hello Prof. Gertraud,
Thank you so much for the great work. I have a question concerning the elliptical equation used to represent the state of the boundary surface of the cam clay model, may you please guide me to the source of this equation?
Thank you!
Ahmed S. Kamel
PhD Researcher
Hi Ahmed,
thank you for your feedback.
I added some comments to it and uploaded the script to create the state boundary surface of the MCC model in stress space:
https://soilmodels.com/wp-content/uploads/2020/12/sbsMCC.txt
The surface has been created using: https://asymptote.sourceforge.io
Just use the Asymptote Web Application and paste the lines in here:
http://asymptote.ualberta.ca/
Was this the surface you were interested in?
A description of the MCC model and equations can e.g. be found in
(i) Muir Wood (1990), Soil Behaviour and Critical State Soil Mechanics, Cambridge University Press,
(ii) Muir Wood (2003), Geotechnical modelling, CRC Press
Kind regards,
Gertraud
Hi Gertraud,
Could you please provide the programming code for “3D view of the Normal Compression Line (NCL), Critical State Line (CSL) and State Boundary Surface of the MCC model “? Thank you.
Best wishes,
Alaa
Hi Gertraud,
Thanks a lot for investing time for clarifications, this is a very appreciated efforts, actually I meant the cam clay model in p’, q, v space. I think I will figure it out from the mentioned sources.
Thank you again for your prompt answer!
Kind regards,
Ahmed.
Hi Alaa, hi Ahmed,
sorry for the late reply.
Here, I uploaded the script for the state boundary surface of the MCC model in p’-q-e space:
https://soilmodels.com/wp-content/uploads/2020/12/sbs_MCC_pqe_soilmodels.txt
The surface has been created using: https://asymptote.sourceforge.io
Just use the Asymptote Web Application and paste the lines in here:
http://asymptote.ualberta.ca/
Kind regards,
Gertraud
Hello Prof. Gertraud,
Thank you so much for the great work. I have a question concerning the elliptical equation used to represent the state of the boundary surface of the bounding surface plasticity model, may you please guide me to the source of this equation?
Thank you!
Riyad
Ph.D. Researcher
Hello Riyad,
Thanks for your feedback.
If you are looking for the state boundary surface of the Modified Cam Clay model, the comments above should help. For a description of the MCC model and related equations, I suggest: Muir Wood (1990), Soil Behaviour and Critical State Soil Mechanics, Cambridge University Press
Regards, Gertraud
Thanks a lot for your reply, Prof. Gertraud. Actually, I am looking for the details of the bounding surface plasticity model (initially developed by Prof. Yannis Dafalias). Have you developed any script for the state boundary surface of the bounding surface plasticity model in the p’-q-v space during drained loading?
Thanks for clarification. Sorry, I didn’t read your question properly.
So far, I have not been dealing with the boundary surface plasticity model.
If I will, I will come back to your questions.
All the best, Gertraud
Hello Prof. Gertraud,
You draw very beautiful graphics, which enable very intuitive understanding of the model’s abilities. As a beginner in hypoplastic model, I would like to ask about the 3D failure surface of clay hypoplastic models. Your 3D failure surface is shaped like a bullet, while mine is a cone. What I don’t understand is how to draw a bullet-shaped damage surface. Could you please guide me on how to do that? It would be even better if you could share your 3D failure surface program for hypoplastic.
Thank you very much!
Wei Li
Ph.D. Researcher
Hi Wei Li,
first of all: sorry for my late reply. I have somehow missed your message.
Here, I uploaded a script to create the asymptotic state boundary surface of clay hypoplasticity stress space:
https://soilmodels.com/wp-content/uploads/2020/12/soilmodels_asbs_hypo_stress_space.wgl
Just use the Web Application of the software Asymptote and paste the lines in here:
http://asymptote.ualberta.ca/
Was that the surface you were interested in?
Kind regards & thank you for your feedback,
Gertraud
Hello Prof. Gertraud,
Thank you so much for the great work.
please can i use SANISAND-MSf model in Abaqus?